Gegeben ist eine Funktion- Errichten sie die Normale im Punkt P=(2/f(2)) des Graphen von f.

Question

vielleicht kann mir hier jemand weiterhelfen:

Gegeben ist die Funktion f (x) = x²/2 + 3

Errichten sie die Normale im Punkt P=(2/f(2)) des Graphen von f.

Wie mach ich denn das :O
Vlt. könnte mir das jemand detailliert beschreiben....
Liebe Grüße

Answer 1

Was kannst du denn schon?

Differenzialrechnung?

Eine Normale zu einem Graphen in einem Punkt P steht senkrecht auf der Tangenten an den Graphen in diesem Punkt. Für die Steigungen m1 und m2 zweier senkrecht aufeinander stehender Geraden aber gilt:

m1 * m2 = - 1

Ist m1 bekannt, dann gilt also: m2 = - 1 / m1

Die Steigung der Tangenten an den Graphen von f ( x ) an der Stelle 2 ist gleich dem Wert der Ableitung von f ( x ) an dieser Stelle, also gleich f ' ( 2 ). Daher ist die Steigung m der gesuchten Normalen:

m = - 1 / f ' ( 2 )

Wegen f ' ( x ) = x  ist f ' ( 2 ) = 2, somit:

m = - 1 / 2

Damit kann die Gleichung der Normalen schon mal soweit hingeschrieben werden:

g ( x ) = - 0,5 * x + b

 

Den y-Achsenabschnitt b ermittelt man so: Da die Gerade durch den Punkt ( 2 | ( f ( 2 ) ) = ( 2 | 5 ) muss die Gleichung g ( x ) für diese Koordinaten erfüllt sein, also:

5 = - 0,5 * 2 + b = - 1 + b

Auflösen nach b ergibt:

b = 5 + 1 = 6

Somit lautet die gesuchte Normalengleichung:

g ( x ) = - 0,5 x + 6

 

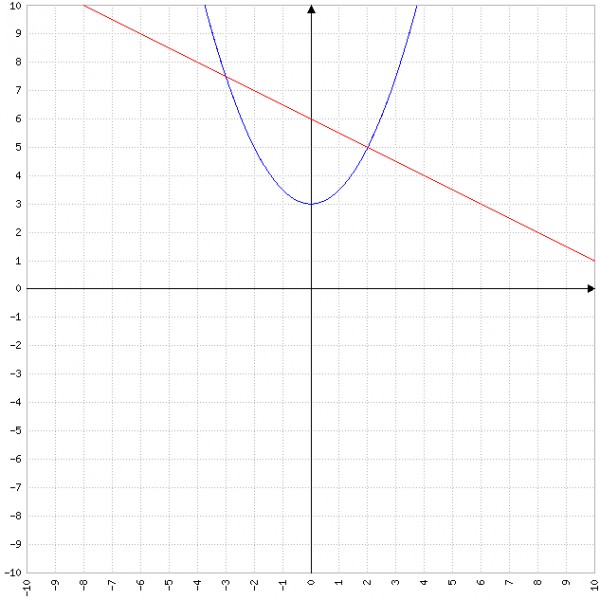
Hier ein Schaubild mit den Graphen von f ( x ) (blau) und der Normalen g ( x ) (rot). Man erkennt, dass g ( x ) im Punkt ( 2 | f ( 2 ) ) = ( 2 | 5 ) senkrecht auf f ( x ) steht: