ich habe Probleme bei folgender Aufgabe:
Betrachten Sie die Folge (an)n≥1 mit an=
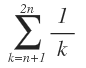
Weisen Sie nach, dass die Folge nach oben beschränkt ist.
Ich verstehe die Aufgabe überhaupt nicht und komme nicht mal auf einen Ansatz, da die Beschränkung bei Reihen eine große Schwierigkeit für mich ist.
Ich bedanke schon mal für jede Hilfe!