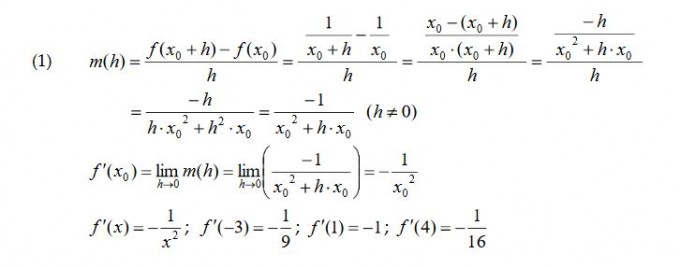h-Methode um Ableitungsfunktion von f(x) = 1/x zu bestimmen? Schritte 1 bis 4?

Question

hierzu bitte eine Erklärung

ich habe diese Aufgabe hier. Leider komme ich nicht weiter, da mir der Rechenweg unklar ist.

Wie komme ich vom ersten Schritt auf den zweiten und vom zweiten auf den dritten und vom dritten zum vierten?

Kann mir hier jemand das besser erklären?

 

Answer 1

f(x)=1/x dann ist f(x+h)=1/(x+h) und der DQ= [1/(x+h)-1/x)] / h Der Zähler [1/(x+h)-1/x)] wird auf den Hauptnenner x(x+h) gebracht und addiert(siehe vorletzter Bruch in der ersten Zeile). Der dort entstandene Doppelbruch wird im Zahler des Zählers vereinfacht: x-(x+h)=-h.

Beim Übergang in die 2.Zeile ist zunächst Bruchrechnung erforderlich: Ein Bruch wird durch h geteilt , indem man den Nenner mit h multipliziert. Dann wird gekürzt -h/h=-1. Zum Schluss wird der Limes gebildet. Das Produkt h·x für h gegen 0 geht ebenfalls gegen 0.

Answer 2

Was hast du gegeben ?
Du hast die die folgende Funktion: f(x) = 1/x  

Was sollst du machen ?
Du sollst mithilfe der sogenannten "h-Methode" die Ableitungsfunktion bilden. Dazu brauchst du folgendes:


$$m(h)\quad =\quad \frac { f({ x }_{ 0 }-h)\quad -\quad f({ x }_{ 0 }) }{ h }$$

Doch was ist dein f(x₀+h) und was ist dein f(x₀) ?


Ein möglicher Weg, wie du das machen kannst:

Ich selber gehe immer so vor:

Ich schaue welche Funktion gegeben ist bzw. von welcher Funktion die Ableitungsfunktion gesucht ist und setze für das x in meiner Funktion ein mal x₀+h ein und das andere mal setze ich x₀ ein.
 
Denn dann sind aus der Ursprünglichen Funktion f(x) folgende zwei "neue" Funktionen entstanden die du für die h-Methode brauchst, nämlich f(x₀+h) und f(x₀).

f(x) = 1/x
f(x₀+h) = 1/(x₀+h)
f(x₀) = 1/x₀

Meine gegebene Funktion ist f(x) = 1/x
Ich brauche für die h-Methode noch f(x₀+h) und f(x₀). Du setzt einfach x₀+h und x_o für das "x" in deine Funktion f(x) = 1/x ein.

Das was du bekommen hast, einsetzen
Jetzt musst du das oben für f(x₀+h) und f(x₀) einsetzen, nimmst aber nur den farbigmarkierten teil,
also rechts vom Gleichheitszeichen.

$$m(h)\quad =\quad \frac { \frac { 1 }{ { x }_{ 0 }+h } \quad -\quad \frac { 1 }{ { x }_{ 0 } }  }{ h } $$

Von hier aus musst du eigentlich vereinfachen und den limes gemäss deinem Lösungsweg in deiner Fragestellung fortfahren.




 

Answer 3

Vorausetzung : die h-Methode ist dir bekannt.

m = [ f ( x + h ) - f ( x ) ] / h

f ( x ) = 1 / x
f ( x + h ) = 1 / ( x + h )

Ziel : h soll bei h −> 0 entfallen