Basiswinkelsatz im gleichschenkligen Dreieck mit Vektoren und Skalarprodukt zeigen

Question

Ich sollte beweisen, dass die Basiswinkel in einem gleichschenkligen Dreieck gleich groß sind. Das habe ich mit der Kongruenz von Dreiecken gelöst. 

Jetzt soll ich den selben Beweis aber noch einmal mit Vektoren und Skalarprodukt lösen... Dabei ist der Tipp die Spitze C des Dreieckes ABC als Nullpunkt zu wählen. Nun habe ich irgendwie gar keine Idee. 

Ich weiß, dass ich mit dem Skalarprodukt überprüfen kann, ob zwei Vektoren orthogonal stehen. In meinem Dreieck ABC kann ich die Höhe C einzeichnen und bekomme die Strecke CD, da wären dann ja zwei rechte Winkel. Aber hilft mir das irgendwie weiter warum die Basiswinkel gleich sind? 

Bin gerade leider voll raus aus analytischer Geometrie, hoffe jemand hat einen Tipp für mich? 

Liebe Grüße 

Answer 1

Die beiden Schenkel seien die Vektoren \(\vec{a}\) und \(\vec{b}\) mit den Längen \(a\) und \(b\). Dann ist die Grundseite \(\vec{c}=\vec{a}-\vec{b}\).

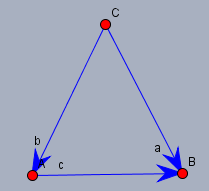
Das Skalarprodukt \(\vec{a}\cdot \vec{c}\) ist

$$\vec{a}\cdot \vec{c}=\vec{a}\cdot\left( \vec{a}-\vec{b}\right)=a^2 - \vec{a}\cdot \vec{b}$$

und das Skalarprodukt \(\vec{b}\cdot -\vec{c}\) ist

$$\vec{b}\cdot -\vec{c}=\vec{b}\cdot -\left( \vec{a}-\vec{b}\right)=- \vec{a}\cdot \vec{b} + b^2$$

Man sieht, dass beide Skalarprodukte gleich groß sind, da \(a^2=b^2\). Es ist aber auch

$$\vec{a}\cdot \vec{c}=a\cdot c \cdot \cos{\beta} \quad \text{und} \quad \vec{b}\cdot -\vec{c}=b \cdot c \cdot \cos{\alpha}$$

(Beachte bei der zweiten Gleichung das Vorzeichen - beide Vektoren zeigen in den Punkt hinein. Wenn sie beide heraus zeigen würden, wäre das identisch!) Und da \(a=b\) ist, müssen auch \(\alpha\) und \(\beta\) gleich sein.

Answer 2

Erst mal eine Skizze ( oben fehlt ein Stück).


Wenn du die Gleichheit der jeweiligen Außenwinkel zeigst, ist es ja auch OK.

Der eine ist der zwischen a und b-a und der andere, der zwischen b und a-b.

Und beim Skalarprodukt gilt ja immer  v*w = |v| * |w| * cos ( winkel dazwischen ).

Also ist wegen der Gleichheit der Längen von a und b und der von a-b und b-a

nur zeigen, dass  a* (a-b) = b * ( b-a )

<==>    a*a  - a*b   =  b*b - b*a

<==>   a*a = b*b   wegen der Längengleichheit erfüllt.