Hallo Jana,
ich weiß jetzt nicht, wo genau Dein Verständnisproblem ist - aber ich versuche es mal:
'normal' bedeutet hier 'senkrecht zu einander'. Zwei Vektoren sind normal zu einander, wenn sie senkrecht auf einander stehen. In diesem Fall ist ihr Skalarprodukt =0.
Zur Demonstration habe ich Dir mal zwei Vektoren gezeichnet - in 2D damit es nicht zu kompliziert wird:
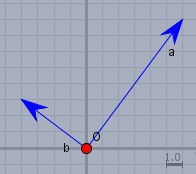
Die Koordinaten haben die Koordinaten
$$\vec{a}=\begin{pmatrix} 6\\8 \end{pmatrix} \quad \vec{b}=\begin{pmatrix} -4\\ 3\end{pmatrix}$$
Skalarprodukt bedeutet nun, jede Koordinate mit jeder korrespondierenden Koordinate des zweiten Vektor zu multiplizieren und dann alle Produkte addieren. Also in diesem Fall
$$\begin{pmatrix} 6\\8 \end{pmatrix} \cdot \begin{pmatrix} -4\\ 3\end{pmatrix} =6 \cdot (-4) + 8 \cdot 3=-24+24=0$$
wie Du siehst, ist das Skalarprodukt =0 und damit ist gezeigt, dass beide Vektoren senkrecht auf einander stehen - also normal zu einander stehen. Wenn noch etwas unklar ist, so frage bitte nach.
Gruß Werner