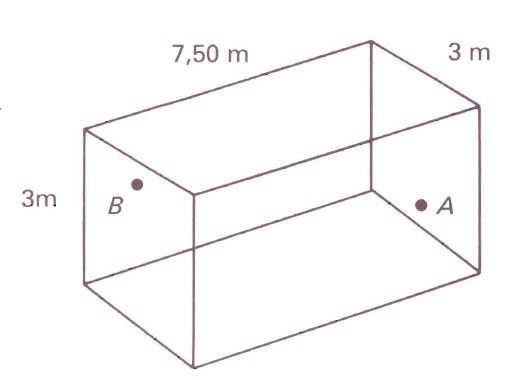
Das Zimmer von Peter ist 7,50 m lang, 3 m breit und 3 m hoch. In der Mitte einer Seitenwand, in A, befindet sich eine Steckdose 25 cm über dem Boden. Um A mit B, das sich in der Mitte der gegenüberliegenden Wand, jedoch 25 cm unterhalb der Decke, befindet, zu verbinden, benötigt er ein Verlängerungskabel.
Der Sicherheit halber kann das Kabel nicht einfach quer durch den Raum gespannt, sondern muss an den Wänden des Zimmers befestigt werden. Wie lang ist das kürzeste Kabel, das Peter benötigt um die Aufgabe zu bewältigen? Nein, 10,50 m ist nicht die richtige Antwort.
Aufgabe: Löse das Problem auf 5 Nachkommastellen.