Kurvendiskussion f(x)= -2x3+3x2-2x+3

Question

Hallo !!!

mich plagt eine Kurvendiskussion  f(x)= -2x³+3x²-2x+3

ich hab bisher irgendwie alle geschaft ausser diese :-(

Sollte da eine Polynomdivision gemacht werden? - hab verschiedene Nullstellen vergeblich versucht..

mit Ausklammern komme ich auf x² - 3/2x +1 = 0  - daraus mit pq-Formel ging nicht...

brauche nullstellen, extrema, Wendepunkte und Graph..

Bitte um Euere Hilfe!

Lilly

Comments

>  .... mit Ausklammern komme ich auf x² - 3/2x +1 = 0  - daraus mit pq-Formel ging nicht...

-2x³ + 3x² - 2x + 3 = 0   ⇔_x≠0    -2x * ( x² - 3/2x + 1 + 3/(-2x) ) = 0 

Da geht natürlich sowieso nichts mit der pg-Formel 

Answer 1

Hi,
wenn man sich ein paar Werte anschaut (wie wenn man eine Wertetabelle aufstellt), so stellt man fest, dass für x = 1 wir ein f(1) = 2 haben und für x = 2 haben wir ein y = -5. Die Nullstelle muss also dazwischen liegen.
In der Tat liegt sie bei x = 1,5.
Hätte man das so nicht gefunden, dann notfalls über ein Näherungsverfahren.

In der Tat haben wir dann keine weitere Nullstellen, deswegen spuckt die pq-Formel auch nichts aus.

f'(x) = -6x² + 6x - 2
f''(x) = -12x + 6

Der Rest sollte ja kein Problem mehr sein?
Sonst nachfragen.

Grüße

Comments

Hallo Lilly,

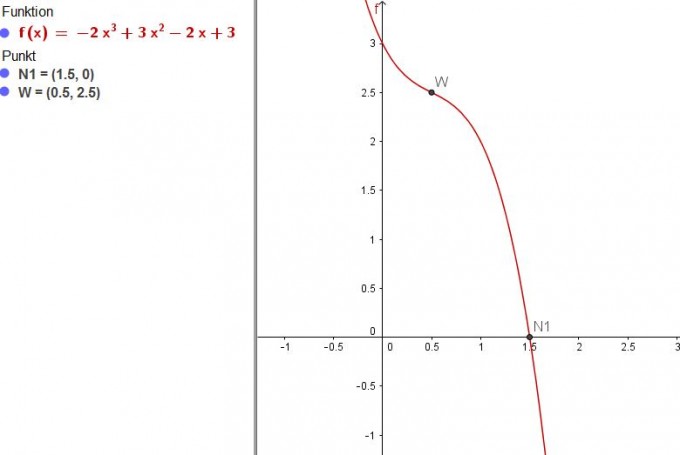
Mit einem Grafik-Taschnrechner wäre es vielleicht auch gegangen. Der hätte dann das Bild angezeigt, woraus sich, wie Unknown schon schrieb, die einzige Nullstelle bei x = 1,5 ergibt.

Ein Extrema gibt es nicht, da

f'(x) = -6x² + 6x - 2

pq-Formel:

$$x_{1,2} = 0,5 \pm \sqrt{ 0,25 - \frac{1}{3} }$$

Der Wert unter der Wurzel ist negativ, also keine Lösung.

Anders sieht es bei den Wendestellen aus:

f''(x) = -12x + 6

-12x + 6 = 0 ⇔ -12x = -6 ⇔ x = 0,5

f'''(x) = -12 ≠ 0

Plotlux öffnen

f₁(x) = -2x³+3x²-2x+3P(0,5|2,5)P(1,5|0)

Answer 2

$$-2x^3+3x^2-2x+3$$

$$= \left( -2x^3-2x \right)+ \left( 3x^2+3 \right)$$

$$= -2x \left( x^2+1 \right)+3 \left( x^2+1 \right)$$

$$= \left( -2x+3 \right) \left( x^2+1 \right)$$

Grüße,

M.B.