Monotonieverhalten untersuchen. Sei f : (0, +∞) → ℝ: x↦ x^x

Question

Sei f : (0, +∞) → ℝ: x↦ x^x

(a) Ist f streng monoton steigend?

(b) Untersuchen Sie f auf lokale Extremstellen.

(c) Untersuchen Sie f auf globale Extremstellen.

Answer 1

f(x)  =  x^x  =  (e^ln(x))^x  =  e^x·ln(x)

Kettenregel und für die innere Ableitung Produktregel:  

f '(x)  =  e^x·ln(x) · (ln(x) + 1)  =   e^x·ln(x) · [ ln(x) + 1) ] ' =   e^x·ln(x) * ( 1 * ln(x + x * 1/x )  

Nach Kommentar von jc2144  korrigiert:

         =  e^x·ln(x)  * ( ln(x) +1)   =  0   ⇔  x = e^-1    mit VZW  von  - →  +   

         →   f ist nicht streng monoton steigend. 

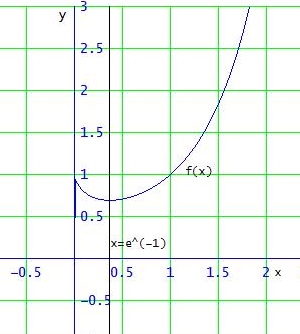
b)    →  T( e^-1 |  e^{- e^{-1}}  ≈  ( 0.3678794411 |  0.6922006275 )      ist lokales  Minimum   

       Wegen   \(\lim_{x \to 0} f(x) \)  = 1 >  f( e^-1)    und    \(\lim_{x \to i∞} f(x) \)  =  ∞

              ist  das auch ein globales Minimum

       ist  das auch ein globales Minimum

 c)  globale und lokale Maxima gibt es nicht.

Gruß Wolfgang

Comments

Mmmh, ist nicht f'(e^{-1})=0 ?

---

Du hast natürlich recht, blöder Fehler. Danke für den Hinweis. Habe das korrigiert.