Monotonie untersuchen von f(x) = x^2/(x^2+1)

Question

bitte um Hilfe bei folgender Funktion: f(x)=x²/(x²+1)

EDIT: Fehlernde Klammern um Nenner ergänzt. 

Answer 1

f(x)=x²/x²+1  wohl eher so   f(x)=x²/(x²+1)

Ableitung   f ' (x) =   f(x)=2x/(x²+1)²

ist für x<0 negativ, also dort f monoton fallend und

für x>0 mon. steigend.

Comments

wie setzte ich die 1. Ableitung gleich null bei gebrochen rationalen fkt?

---

Quotientenregel:

Nenner * Abl. vom Zähler

minus  Zähler mal Ableitung vom Nenner

das Ganze durch Nenner hoch 2.

Und ein Bruch ist nur 0, wenn sein Zähler 0 ist.

---

okay das habe ich, aber wie komme ich dann auf die Nullstellen? Zähler null setzten?

---

setze ich 2x=0   ?

---

genau und  2x=0

  <==>    x = 0

also einzige Nullstelle bei 0

---

danke dir! das hilft schon weiter

Answer 2

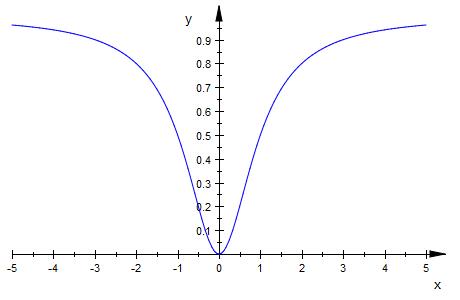
f ( x ) = x² / ( x²+1 )

Nullstellen
x^2 = 0
x = 0

( 0 | 0 )

Monotonie / 1.Ableitung

( u / v ) ´ =  ( u´ * v - u * v´ ) / v^2

x² / ( x²+1 )

u = x^2
u ´= 2x
v = x^2 - 1
v ´= 2x
v ^2 = ( x^2 + 1 ) ^2

( x² / ( x²+1 ) ) ´ =  ( 2x * ( x^2 + 1 ) - x^2 * 2x ) /  ( x^2 + 1 ) ^2

=( 2x^3 + 2x - 2x^3 ) / ( x^2 + 1 ) ^2
= 2x / ( x^2 + 1 ) ^2

Stelle mit waagerechter Tangente
2x / ( x^2 + 1 ) ^2 = 0
2x = 0
x = 0

Monotonie positiv ( steigend )
2x / ( x^2 + 1 ) ^2 > 0

Der Nenner ist durch Quadrat immer postiv
Ist der Zähler auch positiv ist der Bruch
insgesamt positiv
2x >  0
x > 0

Für x > 0 ist die Funktion steigend
Für x <0 ist die Funktion fallend.

x = 0 ist ein Tiefunkt

Comments

2x=0 ist x=0 ? bin gerade völlig verwirrt , wahrscheinlich weil es zu einfach ist!

---

2 * x = 0  | : 2
x = 0 / 2
x = 0

Oder in Worten :
welche Zahl mit 2 multipliziert  ergibt 0 ?