hallo Maarion,
da es sich bei f(x) = x^2 um die Normalparabel handelt, ist der Schnittpunkt mit der x- sowie mit der y-Achse der Ursprung.
Um de Schnittpunkte mit den Graphen aus a), c) und d) zu ermitteln, setzt du die Funktionsterme = x^2 und löst nach x auf:
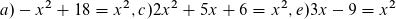
Du erhältst dann folgende Ergebnisse:
a) A (-3|9), B (3|9)
b) A (-3|9), C (-2|4)
d) keine Schnittpunkte
Gruß
Silvia