Zu (a)
Eine Parabel mit Scheitelpunkt auf der y-Achse wird durch die Funktion \( f(x,a,b) = a x^2 +b \) beschrieben. Die Summe der quadratischen Abweichungen lautet
$$ (1) \quad F(a,b) = \sum_{i=1}^n \left( f(x_i) - y_i \right)^2 = \sum_{i=1}^n \left( a x_i^2 + b - y_i \right)^2 $$
(1) wird minimal wenn gilt $$ \frac {\partial F}{\partial a} = 0 \text{ und } \frac {\partial F}{\partial b} = 0 $$
Zu (2)
Das Vorgehen ist das gleiche, nur sieht die Parabel jetzt folgendermassen aus \( f(x,a,b,c) = a x^2 + b x + c \) D.h. hier muss man nach drei Parametern ableiten und die entsprechenden Gleichungen lösen.
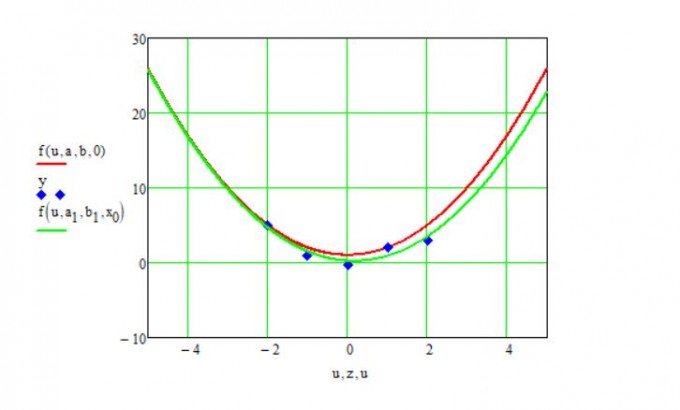
Und so sehen die Kurven dann aus.