Hallo immai,
alles, was jetzt kommt, ohne Gewähr.
(a) Zunächst ist eine Potenzreihe allgemein definiert als
$$f(z)=\sum_{n=0}^\infty a_n(z - z_0)^n$$
wobei \(z_0\) der Entwicklungspunkt ist. Folglich ergeben sich für \(f(z)\), \(g(z)\) und \(h(z)\) die Entwicklungspunkte
f) \(z_0=0\), g) \(z_0=7i\) und h) \(z_0=\frac{4i-1}{2i}=2+\frac{1}{2}i\) (.. siehe auch Lus Kommentar)
Die Konvergenzradien \(\rho\) lassen sich nach dem Quotientenkriterium oder dem Wurzelkriterium bestimmen: Quotienkriterium für \(f\):
$$f(x)=\sum_{n=1}^\infty \frac{\sqrt{n}}{3^n} z^n \quad \Rightarrow a_n=\frac{\sqrt{n}}{3^n} $$$$a = \lim_{n \to \infty} \left| \frac{a_{n+1}}{a_n} \right|= \lim_{n \to \infty} \left| \frac{\frac{\sqrt{n+1}}{3^{n+1}} }{\frac{\sqrt{n}}{3^n} } \right|= \lim_{n \to \infty} \frac{\sqrt{n+1}}{3 \sqrt{n}}=\frac{1}{3}$$
Die Betragstriche kann man hier weglassen, da die Terme jeweils positiv und reell sind. Mit \(\rho=\frac{1}{a}\) wird der Konvergenzradius \(\rho=3\). Mit dem Wurzelkriterium geht es wie folgt:
$$a=\lim_{n \to \infty} \sqrt[n]{|a_n|}= \lim_{n \to \infty} \sqrt[n]{ \frac{\sqrt{n}}{3^n}} = \lim_{n \to \infty} \frac{1}{3} \sqrt[n]{\sqrt{n}}= \frac{1}{3}$$und das ist zum Glück das gleiche Ergebnis.
Bei \(g(z)\) liefert das Wurzelkriterium \(a=0\) bzw. den Konvergenzradius \(\rho=\infty\) und bei \(h(z)\) ist
$$a_n=\frac{(2i)^n}{n^2} \quad \Rightarrow a=\lim_{n \to \infty} \left| \frac{\frac{(2i)^{n+1}}{(n+1)^2}}{\frac{(2i)^n}{n^2}} \right| =\lim_{n \to \infty} \left| 2i\frac{n^2}{(n+1)^2} \right|=2$$ Daraus folgt \(\rho=\frac{1}{a}=\frac{1}{2}\).
(b) Die Kreise werden skizziert, indem Du in der Gaußschen Zahlenebene um den Entwicklungspunkt einen Kreis mit dem Konvergenzradius ziehst.
(c) In der Skizze habe ich die Konvergenzkreise für \(f(x)\) (blau) und \(h(x)\) (grün), so wie die Punkte \(z=2+i\), \(z_2=2\) und \(z_3=3\) eingezeichnet
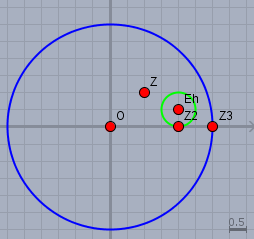
Es ist ersichtlich, dass \(f(1+i)\) konvergiert (liegt innerhalb des Kreises) und \(h(1+i)\) konvergiert nicht. \(g(z)\) konvergiert für jedes \(z\), da dort \(\rho=\infty\) ist.
(d) \(z_2=2\) liegt auf dem Konvergenzkreis von \(h(z)\). Dies muss extra untersucht werden.
$$h(2)=\sum_{n=1}^\infty \frac{(2i\cdot 2 - 4i + 1)^n}{n^2}=\sum_{n=1}^\infty \frac{ 1}{n^2} $$ das ist eine allgemeine harmonische Reihe mit \(\alpha=2>1\) und die konvergiert.
(e) \(z_3=3\) liegt ebenso auf dem Kreis von \(f(z)\). Es ist
$$f(3)=\sum_{n=1}^\infty \sqrt{n} \frac{3^n}{3^n}=\sum_{n=1}^\infty \sqrt{n}$$ und diese Reihe divergiert. \(f(3)\) ist nicht konvergent.
Gruß Werner