Hallo immai,
wenn die Gleichung keine Lösung liefert, so bedeutet das, dass die Ausgangsungleichung entweder für alle oder für kein \(t\) erfüllt ist. In diesem Fall von
$$|i-\sqrt{7} + it| \le \frac{1}{4}$$
erfüllt kein Wert für \(t\) die Gleichung, wenn \(t \in \mathbb{R}\) ist! Das kann man durch probieren ermitteln (z.B. für \(t=-1\)) oder man macht sich eine Skizze
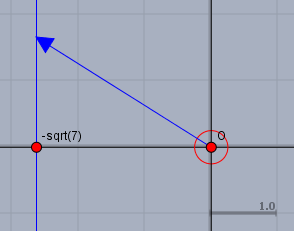
Skizziert habe ich hier die Gaußsche Zahlenebene mit \(O\) als Ursprung. Alle Zahlen innerhalb der Betragsstriche befinden sich auf der blauen Senkrechten. Als Beispiel habe ich einen der Werte mit dem blauen Pfeil gekennzeichnet. Um die Ungleichung zu erfüllen, müsste sich der Pfeil aber innerhalb des roten Kreises mit \(r=1/4\) befinden. Es ist offensichtlich, dass das nicht möglich ist.