Beweise im Dreieck Mittelsenkrechte Höhen Höhenschnittpunkt Mittendreieck

Question

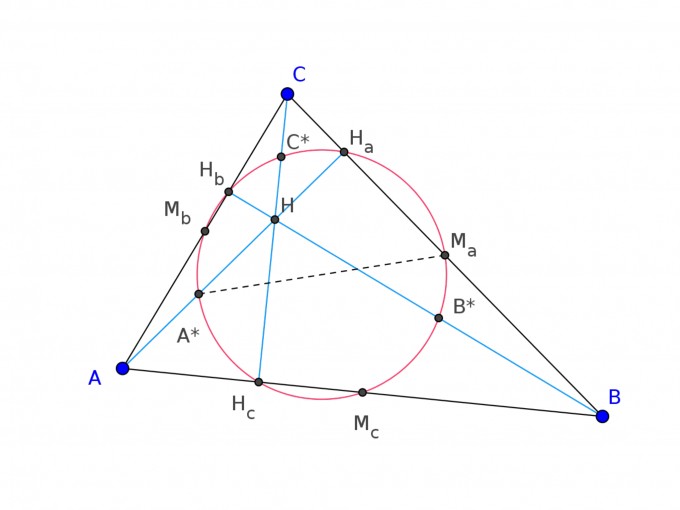
Gegeben ist ein Dreieck ABC mit Höhenschnittpunkt H. A*,B*, C* sind die Mittelpunkte der Strecken AH, BH bzw. CH. Ma,Mb,Mc bilden das Mittendreieck. 

Nun soll ich in a) zeigen, dass A*Mb parallel zu CH= Höhe durch C ist.

Anschaulich natürlich klar, aber ich habe wirklich keine Idee wie ich an diesen Beweis herangehen soll? Ich weiß, dass CH orthogonal auf AB steht und ich weiß dass A*= 1/2 AH und Mb=1/2 AC

Aber was soll ich damit anfangen. Die anderen Aufgaben sind halt alle ähnlich.

B) Zeigen, dass A*Mb orthogonal zu MbMa

C) für den Thaleskreis f über A*,Ma gilt Mb∈f

D) Mc ∈f, d.h. F ist der Umkreis des Mittendreiecks

E) der Lotfußpunkt Ha= ha∩BC liegt auf f

F) B*, Hb und auch C*, Hc liegen auf f

Ich denke mal c-f haben mit dem Feuerbach Kreis zu tun. Aber ich brauche einfach einen Ansatz wie ich an diese Art Aufgaben herangehen soll.

Answer 1

Hallo rosakatze,

a) zeigen, dass A*Mb parallel zu CH= Höhe durch C ist.

"... aber ich habe wirklich keine Idee wie ich an diesen Beweis herangehen soll?"

Lasse zunächst mal alles andere weg, was hier keine Rolle spielt:

"Ich weiß, dass CH orthogonal auf AB steht und ich weiß dass A*= 1/2 AH und Mb=1/2 AC" - völlig richtig Du bist ganz dicht dran. Die Strecke \(A^*M_b\) ist die Mittelparallele zu \(HC\) im Dreieck \(AHC\) - und damit ist schon gezeigt, dass \(A^*Mb\) parallel zu \(HC\) verläuft.

b) \(M_b M_a\) ist die Mittelparallele zu \(AB\) im Dreieck \(ABC\). Und da \(A^*M_b\) parallel zu \(HC\) verläuft und \(HC\) per Definition senkrecht auf \(AB\) steht, so verläuft auch \(A^*M_b\) senkrecht zu \(M_b M_a\).

c) aus dem oben gesagten folgt, dass \(A^*M_b\) senkrecht auf \(M_b M_a\) steht. Folglich ist jeder Kreis von jeder Verbindung zweier Punkte auf den beiden Schenkeln ein Thaleskreis, der den Schnittpunkt \(M_b\) enthält.

.. versuch's mal weiter alleine. Ideen zu weiteren Zusammenhängen gibt es hier: http://www.matheraetsel.de/texte/feuerbach-kreis-main.pdf.

Gruß Werner

Comments

Danke, das hat mir schonmal viel weiter geholfen!!

Habe mir das jetzt so überlegt:

e) Da AH die Höhe ist, steht AH orthogonal auf BC, der Winkel zwischen MaHaA* ist also 90 Grad. Daher ist das Dreieck A*MaHa rechtwinklig mit dem rechten winkel in Ha. Mit der Umkehrung des Satz des Thales gilt dann, dass Ha auf dem Kreis mit dem Durchmesser A*Ma liegt.

f) Hier weiß ich jedoch wieder nicht weiter. Egal wo ich anfange, ich bleibe immer an einer Stelle stehen und komme nicht weiter.

Ob C* auf Kreisbogen liegt: Heißt ja, dass MaC* orthogonal auf C*A* stehen muss.... Es gilt, dass die Höhe Hb orthogonal auf AC steht. AC ist parallel zu MaMc und C*Ma ist parallel zu BH (da MaC* in Dreieck BCH die Mittenlinie ist). Daraus folgt dann, dass MaC* orthogonal auf McMa steht, was mir ja aber nicht wirklich hilft.

Auch bei B* komme ich nicht voran. B*Ma ist zu CH parallel (folgt aus a), daraus folgt dass B*Ma orthogonal zu MbMa ist. Aber daraus kann ich ja nicht direkt was folgern, da ich ja im Punkt B* ein rechten Winkel im Dreieck MaA*B* haben muss, oder nicht?

Vielleicht weißt du ja noch eine Antwort?

---

e) ist richtig.

f) zu \(C^*\): \(C^*M_a\) ist Mittelparallele von \(HBC\) und somit parallel zu \(HB\). Und \(A^*C^*\) ist Mittelparallele von \(AHC\) - also parallel zu \(AC\). Somit stehen \(C^*M_a\) und \(A^*C^*\) senkrecht zueinander und \(C^*\) liegt auf \(f\).

zu \(B^*\): Um zu belegen, dass ein Punkt auf dem Thaleskreis liegt, muss man den rechten Winkel in diesem Punkt finden - also hier in \(B^*\).  \(A^*B^*\) ist Mittelparallele zu \(AHB\) also parallel zu \(AB\) und \(B^*M_a\) ist wiederum Mittelparallele zu \(HBC\) also parallel zu \(HC\). \(HC\) und \(A^*B^*\) stehen folglich wieder senkrecht zueinander und \(B^*\) muss also auch auf dem Thaleskreis über \(A^*M_a\) liegen

hast Du d) gelöst?

Gruß Werner

---

Oh super, ja so ergibt das alles Sinn!

Aufgabe d) habe ich wie folgt gelöst:

Es gilt HB steht orthogonal auf AC weil es ja die Höhe ist. Außerdem gilt, dass AC parallel zu MaMc ist und dass C*Ma parallel zu HB ist.

Daraus folgt dann, dass C*Ma orthogonal auf MaMc steht und damit das Dreieck C*MaMc rechtwinklig ist, weshalb MC auf dem Thaleskreis liegt. Analog dazu liegt Ma auch auf dem Thaleskreis und damit ist der Thaleskreis der Umfang des Mittendreiecks MaMbMc.

Jetzt fehlt mir allerdings bei Aufgabe f) noch der Beweis für die Höhenfußpunkte Hb und Hc. Ich habe versucht das analog zu Aufgabe e) zu lösen, jedoch geht das irgendwie nicht.

Für Hc: Ich muss ja einen rechten Winkel im Punkt Hc im Dreieck A*HcMa haben,richtig? Dafür muss A*Hc also orthogonal auf HcMa stehen. Ich weiß, dass AC orthogonal auf HB steht, muss also zeigen dass A*Hc parallel zu HB liegt und HcMa parallel zu AC, weil ich dann ja folgern kann dass A*Hc orthogonal zu HcMa.

Ich versuche also A*Hc parallel HB zu beweisen, indem ich wieder Mittelparallelen in einem Dreieck suche - nur finde ich keine? Welches Dreieck soll ich dazu wählen?

Gleiches Problem habe ich bei Hb.....

---

Dein Beweis zu d) ist leider keiner. Zunächst mal ist -  wenn man die Aufgabe Schritt für Schritt abarbeitet - zu diesem Zeitpunkt nicht belegt, dass \(C^*\) überhaupt auf \(f\) liegt. Das erfolgt spätestens bei Unterpunkt f). Zum anderen ist \(M_c\) im Dreieck \(C^*M_aM_c\) ein Eckpunkt ohne(!) den rechten Winkel. Dieser Punkt muss also keineswegs auf dem Thaleskreis liegen, wenn die anderen beiden darauf liegen.

"Für Hc: Ich muss ja einen rechten Winkel im Punkt Hc im Dreieck A*HcMa haben,richtig?" Da ist ein rechter Winkel, aber ich halte das an dieser Stelle nicht für zielführend - das ist eher Ergebnis als die Voraussetzung. Besser man nimmt die Dinge, die man bereits hat.

An dieser Stelle der Beweisführung (und genau dass soll wohl mit dieser Aufgabe geübt werden) ist bereits belegt, dass \(H_a\) auf dem Umkreis des Mittendreiecks \(M_a M_b M_c\) liegt. Dann muss dass für die beiden anderen beiden Höhenfußpunkte \(H_c\) und \(H_b\) genauso gelten. Ein allgemeines Dreieck hat ja keine Präferenzen gegenüber einer seiner drei Seiten oder einem seiner Höhenfußpunkte.

Du kannst es aber auch (fast) analog zu e) machen: Zunächst zeigt man über die Mittelparallelen, dass die Punkte \(A^*McM_aC^*\) ein Rechteck bilden. Folglich ist der Mittelpunkt von \(C^*M_c\) identisch mit dem Mittelpunkt von \(A^*M_a\), was gleichzeitig der Mittelpunkt von \(f\) ist. Demnach ist \(f\) auch Thaleskreis über \(C^*M_c\).

Dann geht es weiter wie gehabt: Du schriebst: "Da \(AH\) die Höhe ist, steht \(AH\) orthogonal auf \(BC\), der Winkel zwischen \(M_aH_aA^*\) ist also 90 Grad. Daher ist das Dreieck \(A^*M_aH_a\) rechtwinklig mit dem rechten Winkel in \(Ha\)." Nehme jetzt für jeden Buchstaben 'abc' jeweils den vorhergehenden - dann steht da: "Da \(CH\) die Höhe ist, steht \(CH\) orthogonal auf \(AB\), der Winkel zwischen \(M_cH_cC^*\) ist also 90 Grad. Daher ist das Dreieck \(C^*M_cH_C\) rechtwinklig mit dem rechten Winkel in \(Hc\)." \(M_c\) war schon im Unterpunkt d) dran und \(C^*\) hatten wir schon (s.o. mein Kommentar). Womit belegt wäre, dass \(H_c \in f\) ist.

Gruß Werner

---

Hallo rosakatze,

noch ein Goody:

Die 6 Mittelpunkte bilden drei Rechtecke (s.Skizze) jede Seite eines der Rechtecke ist eine Mittelparallele eines Dreiecks; womit sich jeweils zeigen lässt, dass es sich um Rechtecke handelt. Je zwei gegenüberliegende Punkte eines der Rechtecke liegen also auf einem Durchmesser von \(f\), womit umgekehrt für diese beiden Punkte \(f\) der Thaleskreis ist.

das sollte reichen, die gesamte Aufgabe gut zu lösen.

Gruß Werner

---

"Mathe-Sprache", Skizzen, Erklärungen - höchstes Niveau für mich!

---

Vielen, vielen Dank für die ganze Hilfe! Das hat mir echt weiter geholfen, hätte die Aufgabe sonst echt nicht lösen können, danke!!