Exponentialverteilung Gedächtnislos. EDIT: In der Frage soll es heißen P(X<=3 | X >=2)

Question

Als Beispiel aus der Vorlesung haben wir (X exponentialverteilt mit $$F(x)=1-e^{-\lambda\cdot x},\lambda=1$$). Dann gilt wegen der Gedächtnislosigkeit der Exponentialverteilung

$$P(X\leq2\mid X\geq1)=\dfrac{P(1\leq X\leq2)}{P(X\geq1)}$$ und da kommt dasselbe raus wie für $$P(X\leq 1)$$ Warum geht das nicht für $$P(X\leq3\mid\geq3),\lambda=0.5$$ Wie kann man diesen Wert mit der Gedächtnislosigkeit lösen?

1000 Dank!

Edit: In der Frage soll es natürlich heißen P(X<=3 | X >=2)

Comments

Ah Moment, ich glaube ich bin dumm.

Es gilt doch $$P(X\geq s+ t\mid X\geq s)=P(X\geq t)\Longleftrightarrow P(X\leq s+t\mid X\geq s) = P(X\leq t)$$ Im Beispiel ist $$s=2 \wedge t=1$$ Dann kann ich doch wie oben rechnen, oder?

---

Edit: In der Frage soll es natürlich heißen P(X<=3 | X >=2)

---

EDIT: Habe deine Korrektur oben eingefügt. Hat sich die Frage inzwischen geklärt?

Answer 1

Guten Morgen MathFox,

Du hast bereits richtig erkannt, dass $$P(X\geq s+t\mid X\geq s)=P(X\geq t)\Longleftrightarrow P(X\leq s+t\mid X\geq s)=P(X\leq t)$$ Mit der Angabe $$P(X\leq3\mid X\geq 2)$$ kommt man auch auf die Werte s = 2 und t = 1. Ich werde Dir nun allgemein zeigen, weshalb die Exponentialverteilung überhaupt "gedächtnislos" ist und das Ganze anschließend für Dein Beispiel einmal durchrechnen.

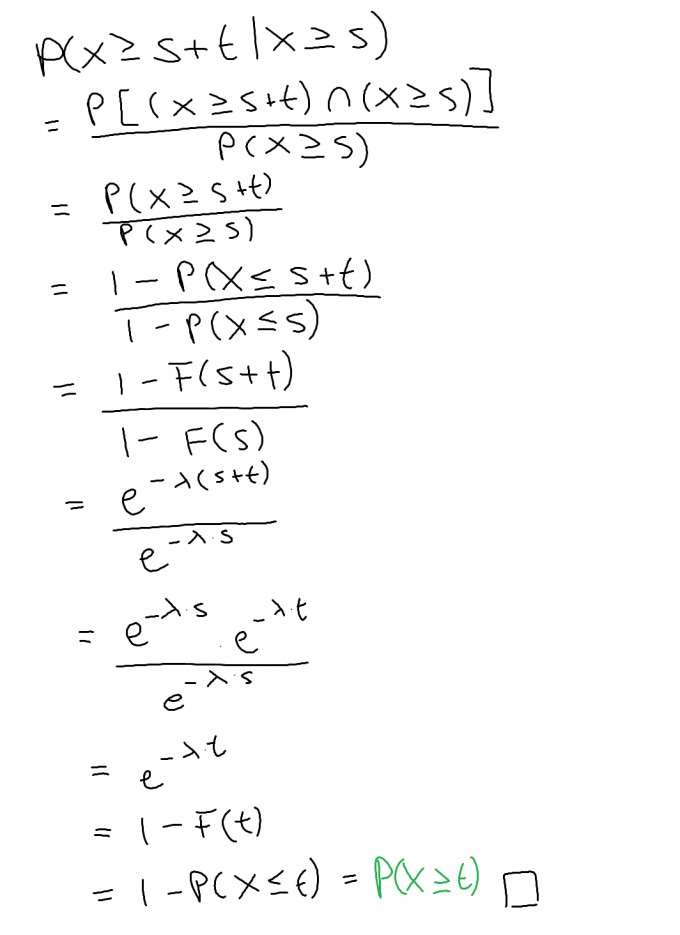
Nun zu Deinem Beispiel. Wenn die Exponentialverteilung tatsächlich gedächtnislos ist (wie oben gezeigt), dann müsste doch gelten: $$P(X\leq 3\mid X\geq2)=P(X\leq 1)$$

Wir berechnen zuerst den Ausdruck auf der rechten Gleichungsseite:

$$P(X\leq1)=F(1)=1-e^{-0.5\cdot 1}\approx0.39$$ Zur Berechnung der Wahrscheinlichkeit auf der linken Gleichungsseite verwenden wir: $$P(X\leq 3\mid X\geq2)=\dfrac{P(2\leq X\leq 2)}{P(X\geq2)}=\dfrac{F(3)-F(2)}{1-F(2)}=\dfrac{(1-e^{-0.5\cdot3})-(1-e^{-0.5\cdot 2})}{1-(1-e^{-0.5\cdot 2})}=\dfrac{e^{-1}-e^{-1.5}}{e^{-1}}\approx 0.39$$

Es kommt in beiden Fällen dasselbe raus, was auch zu erwarten war.

Ich hoffe, dass Dir der Rechenweg/Beweis bei dem Verständnis dieser Aufgabe hilft!

André