weißt Du, wie man Determinanten berechnet? Da das ein Thema für sich ist und da es hier primär um die Cramersche Regel gehen soll, verzichte ich auf die Determinantenberechnung.
1. Bei der Cramerschen Regel bestimmst Du zunächst die Determinante der Matrix, die hinter Deinem Gleichungssystem steht (die Matrix, die sich auf der linken Gleichungssystemseite befindet).
2. Anschließend berechnest Du die Determinanten der Matrizen, die sich dadurch ergeben, dass Du den Vektor b (rechte Gleichungssystemseite) nacheinander in die erste, zweite, dritte und vierte Spalte schreibst.

3. Durch Division dieser Determinanten durch die zuvor berechnete Determinante in 1.), erhältst Du nacheinander die Ergebnisse für $$x_1,x_2,x_3,x_4$$
Es gilt also:
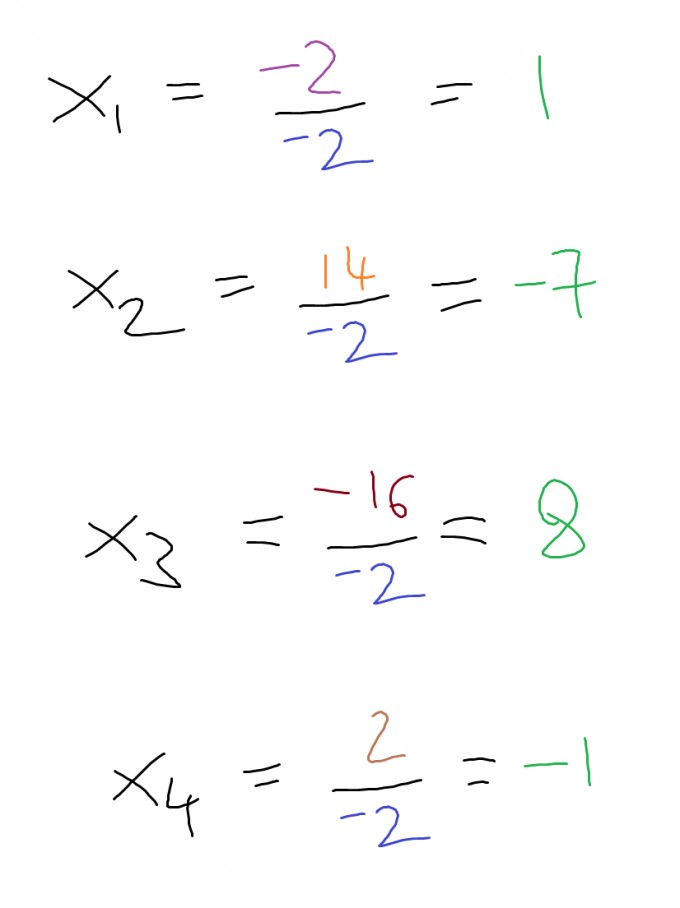
Frage einfach nach, wenn Du etwas nicht verstehst.
Die Ergebnisse der Determinantenberechnung kannst Du hier verifizieren:
https://www.wolframalpha.com/input/?i=determinant+of+%7B%7B1,-1,0,0%7D,%7B2,0,0,-4%7D,%7B0,1,1,0%7D,%7B0,0,1,1%7D%7D
https://www.wolframalpha.com/input/?i=determinant+of+%7B%7B8,-1,0,0%7D,%7B6,0,0,-4%7D,%7B1,1,1,0%7D,%7B7,0,1,1%7D%7D
https://www.wolframalpha.com/input/?i=determinant+of+%7B%7B1,8,0,0%7D,%7B2,6,0,-4%7D,%7B0,1,1,0%7D,%7B0,7,1,1%7D%7D
https://www.wolframalpha.com/input/?i=determinant+of+%7B%7B1,-1,8,0%7D,%7B2,0,6,-4%7D,%7B0,1,1,0%7D,%7B0,0,7,1%7D%7D
https://www.wolframalpha.com/input/?i=determinant+of+%7B%7B1,-1,0,8%7D,%7B2,0,0,6%7D,%7B0,1,1,1%7D,%7B0,0,1,7%7D%7D
