Du weißt sicher, dass man Vekoren i.A. einfach verschieben darf. Also wenn Du nach der Vektorsumme \(a+c\) suchst - ausgehend von \(P\) - so schiebst Du den Vektor \(a\) so, dass sein Anfang in \(P\) liegt und den Vektor \(c\) so, dass sein Anfang an der Spitze von \(a\) liegt. Ist aber \(a-c\) gesucht, drehst Du den Vektor \(c\) um, so dass dieser in die Gegenrichtung zeigt.
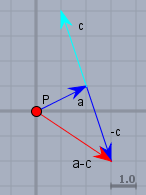
Der hellblaue Vektor wäre \(c\). Wenn dieser in die Gegenrichtung zeigt - bei gleicher Länge - so wird er zu \(-c\). Aneinander gehängt erhält man den roten Vektor \(a-c\).
Genauso geht man bei dem Ausdruck \(2b - \frac{1}{2}d\) vor. Beginne mit dem Vektor \(b\) den Du so verschiebst, dass er mit dem Anfang in \(P\) liegt. Da ein Faktor von 2 davor steht, verländern wir ihn auf das Doppelte. Anschließend wird der Vektor \(d\) an die Spitze von \(2b\) verschoben (blauer Pfeil nach rechts unten) und da er abgezogen werden soll, muss die Richtung invertiert (also umgedreht) werden (der grüne Pfeil). Jetzt zeigt er nicht mehr nach rechts unten, sondern nach links oben. Zuletzt noch den Faktor \(\frac{1}{2}\) berücksichtigen, also wird er nur halb so lang gezeichnet, wie er ursprünglich war.
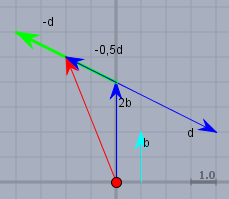
Der rote Vektor ist das Resultat \(2b-\frac{1}{2}d\).
man kann also durch einen vorgestellten Faktor den Vektor in der Länge verändern und wenn der Faktor negativ ist, so wird die Richtung invertiert. So kann man mit dem Ausdruck \(r\cdot b + s \cdot d\) jeden Punkt in einer Ebene erreichen.
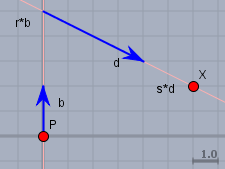
Mit \(r\) kann ich die Spitze von \(r \cdot b\) auf der Senkrechten beliebig verschieben - in dem Beispiel auf den Wert \(2,5 \cdot b\) und anschließend kann ich einen Vekor \(s \cdot d\) anhängen. Und da \(s\) beliebig wählbar ist, kann man nun jeden Punkt anfahren. Hier im Beispiel ist \(x=2,5 \cdot b + 1,5 \cdot d\).
Also kommt man auch zum Vektor \(c\). Es soll sein \(c=r \cdot b + s \cdot d\) - formal schreibt man in vektorieller Darstellung:
$$c = \begin{pmatrix} -1 \\ 3 \end{pmatrix}= r \cdot b + s \cdot d = r \begin{pmatrix} 0 \\ 2 \end{pmatrix} + s \begin{pmatrix} 4 \\ -2 \end{pmatrix} $$
oder als Gleichungssystem
$$-1 = r \cdot 0 + s \cdot 4$$
$$3 = r \cdot 2 + s \cdot (-2)$$Hier muss \(r = \frac{5}{4}\) und \(s=-\frac{1}{4}\) sein. Falls Du nicht weißt, wie man dahin kommt, so frage nochmal nach. Das ganze noch mal graphisch als Kontrolle (nur größer gezeichnet):
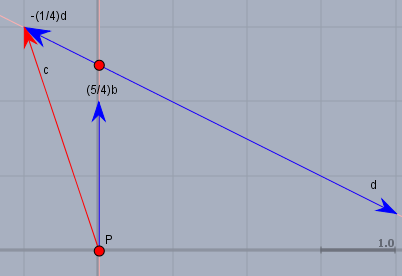
Gruß Werner