EDIT: Kopie aus Kommentar:
Vielleicht hilft es wenn ich konkrete Aufgabenstellung aufschreibe.
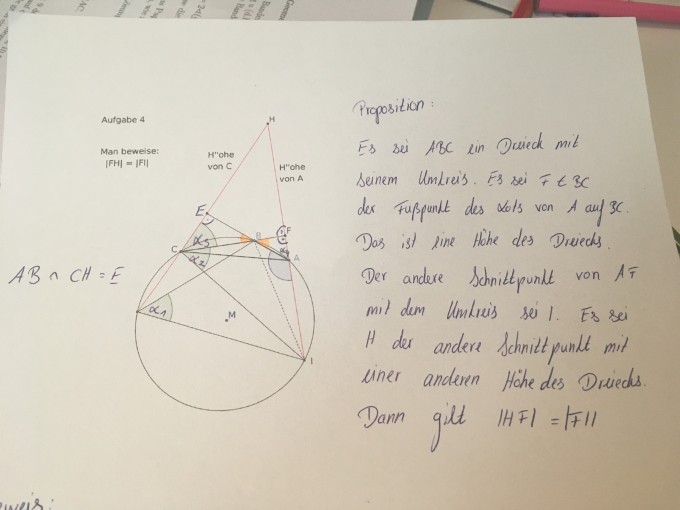
Man beweise die Proposition (im Bild) für den Fall eines stumpfwinkligen Dreiecks ABC, wie es auf der beiliegenden Abbildung gezeichnet ist. Man begründe dazu, warum alle grünen Winkel gleich groß sind.
Ich habe ja bereits Alpha 1 = Alpha 2
und Alpha 3 = Alpha 4
wenn ich zeigen kann dass Alpha 2= Alpha 3 dann habe ich ja 2 gleiche Winkel und die gleiche Seite CF.
Ursprüngliche Version:
Ich soll in der Aufgabe begründen warum die grünen Winkel gleich groß sind. Um die oben stehende Proposition zu beweisen.
Mir fehlt nur noch warum Alpha 1,2 = Alpha 3,4 ist.