Nach nebenstehender Skizze soll ein Tunnel mit einer Querschschnittsfläche von 25m^2 gebaut werden.

Question

Die Aufgabe wurde schon mal gestellt nur ich kann sie nicht nachvollziehen..

Nach nebenstehender Skizze soll ein Tunnel mit einer Querschnittsfläche von \( 25,0 \,\mathrm{m}^{2} \) so gebaut werden, dass die Materialkosten für seine Auskleidung (Umfang des Tunnelquerschnitts) moglichst gering werden.

Berechnen Sie die Breite a und die Höhe \( b \) des Tunnels.

Hinweis:
Drücken Sie in der Funktion für den Tunnelumfang die Höhe \( b \) durch die gegebene Tunnelfläche aus.

Answer 1

Aufgrund des Hinweises komme ich zuerst auf Fläche A = a b + 1/2 pi (a/2)^2 = 25 und somit b = - (pi (a/2)² - 50) / (2a)

Der zu minimierene Umfang (inklusive Boden) ist a + 2b + pi a/2, mit Einsetzen von b wie oben a - 2((pi (a/2)² - 50) / (2a)) + pi a/2 woraus folgt a = 5.29 und b gemäss Formel im ersten Abschnitt.

Comments

Mein Ansatz,, bei mir haberts am umstellen und kürzen

---

Ich hab's Schrittweise aufgeschrieben um mein Fehler besser zu erkennen

---

Ich hab deinen Fehler unten mal markiert.

Answer 2

Hallo Mark,

beim Auflösen nach b hast du mit 4 multipliziert. Dann musst du aber auch a*b mit 4 multiplizieren. Ich schreibe dir meine Rechnung auf:

Wie du schon richtig geschrieben hast:

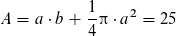
Um nach b aufzulösen subtrahierst du zuerst -1/4 π a^2

Das ist die Gleichung, von der du die erste Ableitung bilden und gleich null setzen musst (notwendige Bedingung für ein Extremum)

Mein Ergebnis für a ist dann 4,79

Kommst du jetzt klar?

Comments

Vielen vielen Dank, ich rechne es morgen nach, das Bett ruft

---

Hallo Silvia,

Leider ist deine Lösung falsch. Siehe die Lösung von döschwo! 

---

Tja, die habe ich gesehen, fnde meinen Fehler aber trotzdem nicht.

---

Ich habe deinen Fehler unten mal markiert.

---

Koffi, du hast recht. Tut mir leid, Mark. Aber hoffentlich ist wenigstens der Rechenweg anschaulich.

---

Stimmt, is ja ein Halbkreis.. aber Danke nochmals für den ausführlichen Rechenweg..