Es handelt sich um folgende Aufgabe:
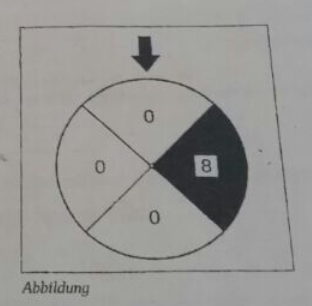
Beim Spiel "Die wilde 8" wird das Glücksrad mit den beiden Zahlen 0 und 8 (s. Abbildung) zweimal gedreht.
a) Erstellen Sie für dieses Zufallsexperiment ein vollständig beschriftetes Baumdiagramm mit allen Pfadwahrscheinlichkeiten.
b) Die beiden Zahlen in den Feldern, auf die jeweils der Pfeil zeigt, werden addiert.
(1) Berechnen Sie die Wahrscheinlichkeiten dafür, dass sich
- die Summe 0 ergibt
- die Summe 8 ergibt
- die Summe 16 ergibt
(2) Der Spieleinsatz für das zweimalige Drehen des Glücksrades Beim Spiel "Die wilde 8" beträgt 8 €.
- Bei der Summe 0 gibt es keine Auszahlung, der Spieleinsatz ist verloren.
- Bei der Summe 8 wird der Spieleinsatz zurückgezahlt.
- Bei der Summe 16 wird der zehnfache Spieleinsatz ausgezahlt.
Der Spielleiter behauptet, das Spiel sei "fair". Das heißt, dass ein Spieler auf lange Sicht weder Gewinn noch Verlust macht.
Untersuchen Sie, ob es sich wirklich um ein faires Spiel handelt.
STehe vor einem Problem undzwar soll ich die Summe der Wahrscheinlichkeiten ausrechnen.
TEil A wäre ein Baumdiagramm mit zwei Pfaden am Anfang einer der Pfade wäre 1/4 für die 8 der andere Pfad 3/4 für die 0. Am Pfad 0 wäre dann wieder eine Verzweigung mit 1/4 für 8 und 3/4 für 0. Am Pfad 8 wäre die Verzweigung 1/4 für die zweite 8 und 3/4 für die 0. Somit hätte ich das Baumdiagramm zu Aufgabenteil a bestimmt. Aufgabenteil b 1) verstehe ich nicht was muss ich addieren und wie gestaltet sich der Erwartungswert von b 2)