folgende Aufgabe:
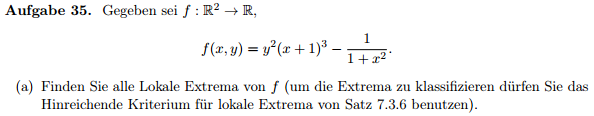
1. Notwendige Bedingung: Der Gradient wird gleich Null gesetzt. Hier habe ich schon ein Problem:
fx= 3x2y2+6xy2+3y2+(2x)/(x2-1)2
fy= 2x3y+6x2y+6xy+2y
Ich muss ja eigentlich beide Gleichungen Null setzen. Für fy folgt dann ja schon der richtige Punkt x=-1 und y=0. Wenn ich dies aber in fx einsetze, dann kommt ja im hinteren Teil -2/0 raus. Durch Null teilen ist ja bekanntlich nicht so optimal. Wie krieg ich das weg?
2. Danach muss ich ja nur noch die Hinreichende Bedingung prüfen, also zeigen dass die Determinante der Hessematrix größer/kleiner Null ist. (In diesem Fall >0, da ein Minimum in (-1/0) angenommen wird. Hier habe ich aber wieder das Problem mit der Null.
Vielleicht kann jemand helfen, danke euch! :)