Gegeben ist das Parallelogramm mit den Eckpunkten A(1/1),B(8/5),C(8/5) und D(2/5).
Vielleicht hat B hier die Koordinaten (7, 1). Wenn nicht bitte noch mitteilen. Das B und C die gleichen Koordinaten haben wäre sehr unwahrscheinlich.
a) Zeichen Sie das Parallelogramm einschließlich seiner Diagonalen in ein Koordinantensystem.
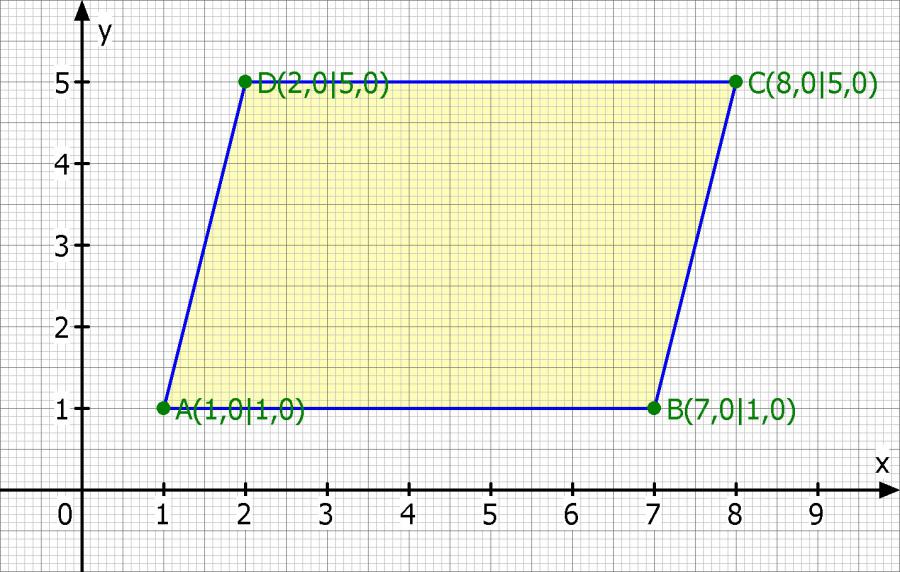
b)Zeichnen Sie die Funktionterme der Funktionen, auf deren Graphen die Diagonale des Parallelogramms liegen.
Diagonale durch A(1/1), C(8,5)
m = (5-1) / (8-1) = 4/7
f(x) = m * (x - Px) + Py = 4/7 * (x - 1) + 1 = 4/7·x + 3/7
Diagonale durch B(7/1), D(2,5)
m = (5-1) / (2-7) = 4 / (-5) = -4/5
g(x) = m * (x - Px) + Py = -4/5 * (x - 7) + 1 = 33/5 - 4/5·x
c) Berechnen Sie den Schnittpunkt der Diagonalen.
f(x) = g(x)
4/7·x + 3/7 = 33/5 - 4/5·x
20·x + 15 = 231 - 28·x
48·x = 216
x = 4.5
y = 33/5 - 4/5·4.5 = 3
Der Schnittpunkt ist (4.5 | 3)
Er ließe sich auch anders ausrechnen. Indem man den Schwerpunkt der 4 Punkte nimmt.
1/4 * ([1, 1] + [7, 1] + [8, 5] + [2, 5]) = [4.5, 3]