Nichtlineares Gleichungssystem mit sin und cos soll genau eine Lösung haben? Wie zeige ich das?

Question

Hallo Community, bei dieser Aufgabe hänge ich leider total :/ ich habe es mit dem Banachschen Fixpunktsatz probiert aber komme auf keine vernünftige Lösung...

Für einen Lösungsansatz wäre ich sehr dankbar! Vielen Dank :)

Zeigen Sie, dass das nichtlineare Gleichungssystem

cos(v ) = u*(cos(u) + 3)^2

sin(u) = v*(sin(v ) + 3)^2

genau eine Lösung auf R² hat.

Hinweis: Sie müssen die Lösung nicht bestimmen!

Comments

Vom Duplikat:

Titel: Nichtlineares Gleichungssystem mit sin und cos soll genau eine Lösung haben ? Wie zeige ich das?

Stichworte: linear,nicht,gleichungssystem,genau,lösung

Ich verstehe nicht, wie ich zeigen soll, dass die Funktionen genau EINE Lösung haben :/ eine Erklärung würde mir sehr helfen!

Answer 1

Vermutlich reicht grobe Parameterdarstellung (zeichnerische Lösung):

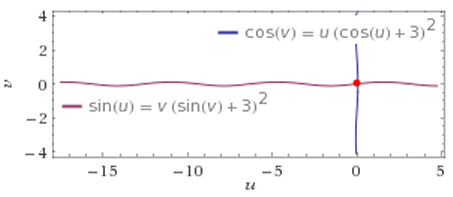
Aber mich interessiert viel mehr der genaue Punkt:

u=asin(v*(sin(v) + 3)²)

cos(v) = asin(v*(sin(v) + 3)²)*(cos(asin(v*(sin(v) + 3)²)) + 3)²=asin(v (3 + sin(v))^2) (3 + sqrt(1 - v^2 (3 + sin(v))^4))^2

numerische Lösung:

v=0.00691463125159320869555427677217704710370371074038272673339996791

Probe1:

0.999976094032577065550403656123478027864=0.999976094032577065550403656123478027864

Probe2:u=asin(v*(sin(v) + 3)²) ,v=0.00691463125159320869555427677217704710370371074038272673339996791

u=0.0625596811240114158016593008004402687121504168614128793236522553

cos(v) = u*(cos(u) + 3)²,u=0.06255968112401141580165930080044026871215041686

=0.99997609403257706555040365612347802786427192463859609090

v=acos(0.9999760940325770655504036561234780278642719246385960909)

v=0.00691463125159320869555427677217704710370371074038273 OK stimmt

Warum es nur 1 Lösung gibt, zeigt die umgestellte Funktion:

sin(u) = acos(u*(cos(u) + 3)²)*(sin(acos(u*(cos(u) + 3)²)) + 3)²

u=asin(acos(u*(cos(u) + 3)²)*(sin(acos(u*(cos(u) + 3)²)) + 3)²) hat nur 1 Punkt ohne Imaginärteil!

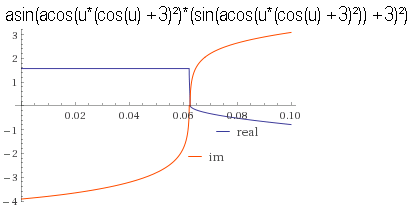
Warum so viele Nachkommastellen:

weil (2 (-1088 - 48 Pi + 129 Pi^2))/(-1384 - 79Pi + 1173 Pi^2)= 0.0069146312515932086955489...

mit 22 Nachkommastellen übereinstimmt, ABER nicht die Lösung ist!