Extremstellen mit Nebenbedingung

Question

ich versuche mich gerade an dieser Aufgabe: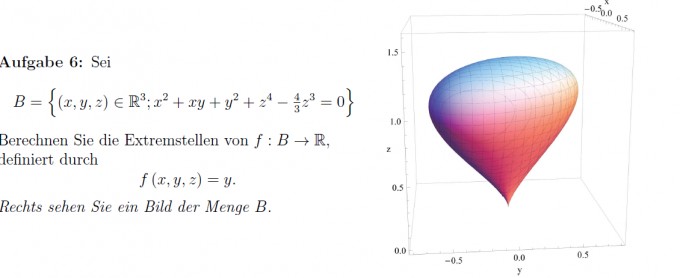 

ich habe jetzt schon mal die partiellen Ableitungen berechnet:

$$ L(x,y,z,\lambda)=y+\lambda (x^2+xy+y^2+z^4-\frac { 4 }{ 3 }z^3) $$

$$L_x'(x,y,z,\lambda)=0+\lambda=0$$

$$L_y'(x,y,z,\lambda)=1+\lambda=0$$

$$L_z'(x,y,z,\lambda)=0+\lambda=0$$

$$L_\lambda'(x,y,z,\lambda)=x^2+xy+y^2+z^4-\frac { 4 }{ 3 }z^3=0$$

Nur weiß ich hier nicht wie ich exakt weiter machen soll. Ich hätte durch die 4 Gleichung auf die Hesse Matrix getippt, bin  mir aber nicht sicher ob es auch anders gehen kann.,

 

lg

Answer 1

Deine partiellen Ableitungen solltest du eventuell prüfen.

L(x,y,z) = y + k·(x^2 + x·y + y^2 + z^4 - 4/3·z^3)

L'x(x,y,z) = k·(2·x + y) = 0

L'y(x,y,z) = k·x + 2·k·y + 1 = 0

L'z(x,y,z) = 4·k·z^2·(z - 1) = 0

Ich komme auf die Lösungen

[x = 1/3 ∧ y = - 2/3 ∧ z = 1 ∧ k = 1, 

x = - 1/3 ∧ y = 2/3 ∧ z = 1 ∧ k = -1]

Comments

Ich dachte hier muss man noch bei \( \lambda\) ableiten?

---

Dann bekommst du ja nur die Nebenbedingung. Da man die ja eh schon notiert hat ist es eigentlich Unsinn nochmals nach Lamda abzuleiten. Kannst du natürlich machen. Ich spare mir das immer. Bisher konnte mir auch keiner sagen warum das nochmals gemacht wird.

---

Ok ich habe das hier jetzt schritt für schritt gemacht, auch mit der Ableitung für das lambda, aber habe hierbei ein Problem : 

$$1. L'x(x,y,z,\lambda) = k·(2·x + y) = 0  \to  x=-y/2$$

$$ 2.L'y(x,y,z,\lambda) = k·x + 2·k·y + 1 = 0 \to  y=\frac{-2}{3}\lambda $$

 also$$ \to  x = -1/3\lambda$$

3.\(L'z(x,y,z,\lambda) = 4·k·z^2·(z - 1) = 0 \to  \)\(z=0  \) oder \(z=1\)

$$ 4.L'\lambda(x,y,z, \lambda)=z^4-\frac{4}{3}z^3+y^2+xy+y^2$$ Setze ich alle meine Werte in 4. ein komme ich auf: 

$$ \frac{5}{9} \lambda^2-\frac{1}{3} \lambda-\frac{1}{3}=0$$

Die letzte Gleichung geht nicht auf, und ich frage mich daher wo mein Fehler ist. 

---

"→x=−1/3λ"

Prüf da mal bitte das Vorzeichen.

---

Ok. Die letzte Gleichung sollte:  $$\frac{3}{9} \lambda^2-\frac{1}{3}=0  $$ lauten, dann bekomme ich ebenso +1 und -1  raus. z=0 ist denke ich hierbei irrelevant also resultiert: bei mir ebenso:

x=1/3 y=-2/3 z=1 für lambda=1 und x=-1/3 y=2/3 z=1 für lambda=-1 

---

Tut mir leid wenn ich das hier Kurzzeitig zum Leben erwecke. Aber ist hier  (0,0,0) nicht auch eine Extremstelle?

Answer 2

So aus dem Bauch heraus, kannst du mit x=0, y=0, z=0 nix falsch machen. Mit der Begründung, das stetige Funktionen auf Kompakten Mengen immer mindestens eine MIN und eine MAX stelle haben, hast du so schon dein lokales Minimum durch die 4. Gleichung L′λ(x,y,z,λ)=x2+xy+y2+z4−43z3=0 nachgewiesen.

Dann müsstest du nurnoch zeigen, das das auch ein Globales Minimum ist. Sollte nicht so schwer sein.

Bei Maximum bin ich mir noch nich so sicher.