Lösung der inhomogenen linearen Differentialgleichungen bestimmen

Question

Hi, könnte mir jemand folgendes erklärend vorrechnen? Danke

Answer 1

alle 3 DGL kannst Du mit dem Verfahren" Variation d. Konstanten " lösen

das allg. Schema lautet:

1. Berechnung der homog. Gleichung:(1.Aufgabe)

-------->

y'  -2y=0  ->Trennung d. Variablen

dy/dx= 2y

dy/y=2 dx

y_h=C₁ e^{2x}

2. y_p= C(x)  e^{2x} ;(dabei setze  C=C(x)

3.) _yp'=

4.Setze y_p und y_p' in die Aufgabe ein

5.)(dabei kann man C(x) kürzen

C'(x)=

C(x)=

6.)y_p= C(x) *e^{2x}

7.)y= y_h +y_p

_8)Lösung:

_{y= C1 e^{2x} +1/4(sin(2x) -cos(2x)}

_{------------------------------------------------------------------------------}

_{Aufgabe b)}

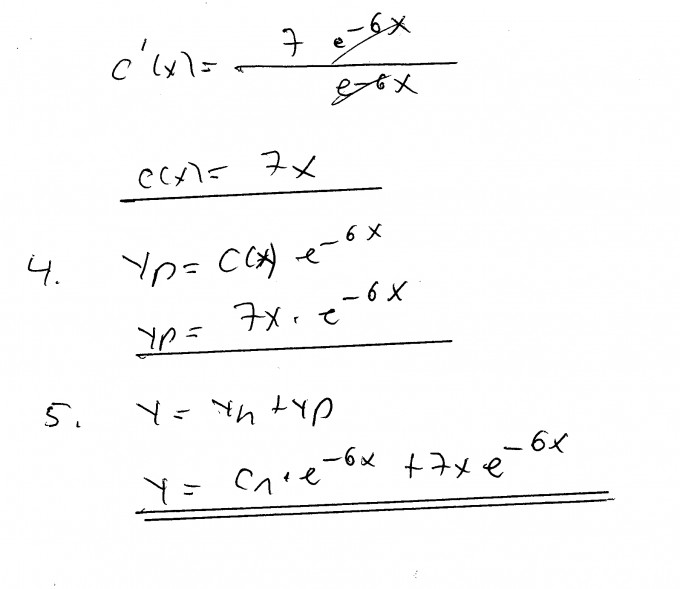
_{Aufgabe c)}