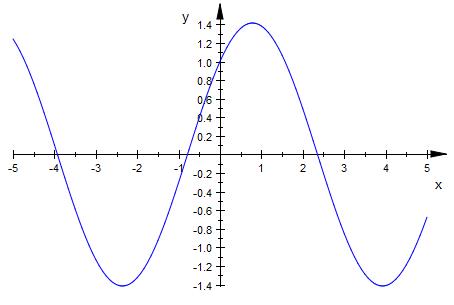
f ( x ) = Sin(x) + Cos(x)
Minimum oder Maximum einer Funktion :
1.Ableitung zu null setzen.
die gefundenen Werte in die Funktion einsetzen
f ´( x ) = cos ( x ) + ( - sin ( x ))
f ´( x ) = cos ( x ) - sin ( x )
Stellen mit waagerechter Tangente
cos ( x ) - sin ( x ) = 0
cos ( x ) = sin ( x )
sin (x ) / cos ( x ) = 1
( sin / cos ) = tan ( allgemein )
tan ( x ) = 1
x = arctan (1 )
x = 0.7854
f ( 0.7854 ) = sin ( 0.7854 ) + cos ( 07854 )
y = 1.4142 ( max )
min findet du sicher auch heraus.