Wertebereich bestimmen von f(x) = sin(4x) / ln(2x+1)

Question

ich habe folgende Funktion vor mir:

$$\frac { sin(4x) }{ ln(2x+1) }$$

und soll den Wertebereich bestimmen. 

Meine Überlegung war das die Amplituden der Funktion immer kleiner werden und somit der erste und zweite Extrempunkt den Wertebereich bestimmen.

also habe ich die erste Ableitung bestimmt und null gesetzt. 

$$\frac { { 4\cos  \left( 4x \right)  } }{ \ln { \left( 2x+1 \right)  }  } -\frac { { 2\sin  \left( 4x \right)  } }{ { \left( 2x+1 \right) \ln { ^{ 2 } } \left( 2x+1 \right)  } } =\quad 0$$

Ab hier komme ich nicht mehr weiter. Ich weiß nicht wie ich umformen soll. 

Answer 1

f '(x)  =  [ 4·(2·x + 1)·LN(2·x + 1)·COS(4·x) - 2·SIN(4·x) ]  /  [ (2·x + 1)·LN(2·x + 1)² ]

Stimmt nicht mit deiner Ableitung überein.

Für eine Lösung mit normalen TR  von

[ 4·(2·x + 1)·LN(2·x + 1)·COS(4·x) - 2·SIN(4·x) ]  /  [ (2·x + 1)·LN(2·x + 1)² ]   =  0

sehe ich keine andere Möglichkeit als ein Näherungsverfahren ( z. B Newtonverfahren).

Dazu müsstest du aber den linken Term noch einmal ableiten, und im Folgenden wären g(x) = f '(x) und g '(x) = f "(x) und jeweils eine Nullstellen von g(x) gesucht:

Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man - auch mit einem einfachen Taschenrechner -  immer bessere Werte mit der Formel

x_neu =  x_alt - g(x_alt) / g ' (x_alt)

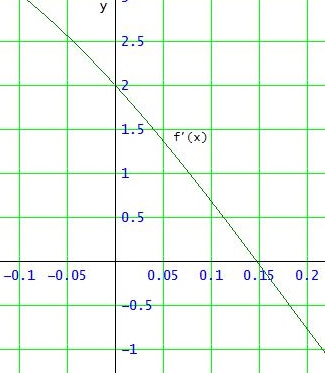
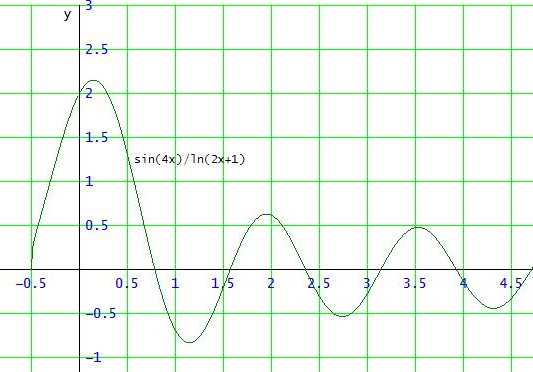
Um  die - wegen der streng monoton abfallenden Amplitude - 1. positive Nullstelle (Maximalstelle von f) zu finden, sollte es dann schon ein Startwert dort in der Nähe sein.

Gruß Wolfgang

Gruß Wolfgang

Comments

Hallo Wolfgang,

Vorab : Hinweis
Für eine händige Lösung von
es muß heißen
Für eine händische Lösung von

Diese  Aufgabe händisch / mit einfachem
Taschenrechner lösen zu wollen wäre
Tierquälerei.

Ich habe mir die höhere Mathematik selbst
durch Rechnen von Abituraufgaben beigebracht.
Dort gab es in einzelnen Bundesländern Aufgaben
bei denen ich gedacht habe : was muß hier
gerechnet werden.

Bis ich den einmal den Hinweis fand : die Aufgaben
sind mit GTR oder CAS zu lösen.

mfg Georg

---

Danke, ist korrigiert.

---

Hallo Wolfgang,

bei Interesse : siehe bei meiner Antwort.

Der Fragesteller sprach davon dies sei eine
Uralt-Frage zu deren Lösung damals kein
CAS / GTR notwendig sei.

Fest steht mittlerweile : die Extrempunkte des Zählers
sin (4x ) stimmen nicht mit den Extrempunkten
der Gesamtfunktion überein ( Stichwort gedämpfte
Schwingung ) .

ich komme bei der Aufgabe einfach nicht weiter.

mfg Georg

---

Hallo Georg,

> Fest steht mittlerweile : die Extrempunkte des Zählers 

sin (4x ) stimmen nicht mit den Extrempunkten 

der Gesamtfunktion überein                                                                                                                       vgl. meinen Kommentar zur Antwort von Mathef  :-)
Gruß Wolfgang

---

@stroganof

wurde die Frage so gestellt ?
Bitte einmal ein Foto einstellen.

Falls die Frage interessenhalber von dir
gestellt wurde dann bitte auch mitteilen.

mfg Georg

Answer 2

1 / ln(2x+1)  ist doch streng mon. fallend und positiv über IR⁺.

Also sind die Extrema dort, wo auch die von sin(4x) sind, also wenn

4x = ( n+0,5)*pi  mit n aus IN.

Fall noch neg. Zahlen zum Definitionsbereich gehören musst du auch der Seite auch über legenund bei -0,5 ist ja eine Definitionslücke.

Comments

> Also sind die Extrema dort, wo auch die von sin(4x) sind.

Das bezweifle ich:

sin( 4 * π/8) = 1   (Hochpunkt, π/8 ist Maximalstelle von sin(4x)

f(π/8) ≈ 1.725204431  <  2.152131787 ≈ f(1.15)

x = π/8 ist also keine Maximalstelle von f

Answer 3

Zunächst einmal der Def-Bereich

sin(4x) / ln(2x+1)

2x + 1 > 0
x > -1/2

Ausschließen ? Division durch 0.
ln ( 2x +1 ) = 0
2x + 1 = e^0  = 1
2x = 0
x = 0

sin(4x) / ln(2x+1)
sin(4x*0) / ln(2*0+1) = 0 / 0
L´Hospital
[ sin(4x) ] ´  / [ ln(2x+1) ] ´
( cos(2x) * 4 ) / [ 2 / ( 2x+1 ) ]
cos(2x) * 4 ) * ( 2x+1 ) / 2
cos(2 * 0 ) * 4 ) * ( 2 * 0 +1 ) / 2
4 / 2 = 2

( 0 | 2 )

Def-Bereich
x > -1/2

Soviel zunächst.

mfg Georg

Comments

Hier einmal der Graph

Der Randwert links wäre

lim x −> -0.5(+)  ( -0.5(+) | 0 )

---

Das wäre ja der  Def-Bereich ich suche aber den Wertebereich also Werte die y annehmen kann. Das wäre wie man auf dem Graph erkennt das erste Maxima und das erste Minimum, da die Funktion für x −>∞ gegen null strebt. Ich dachte ich bestimme die ersten beiden Nullstellen der Ableitung und ermittle so der Wertebereich.  

Die Ableitung wäre:

4cos(4x)ln(2x+1)−2sin(4x)(2x+1)ln2(2x+1)=0
Ich weiß nicht wie man von dieser Funktion die Nullstellen bestimmt. Oder sind meine Überlegungen Falsch?

---

Eine Frage vorab : woher hast du die Aufgabe ?
Darf GTR / CAS zur Lösung genutzt werden ?

---

Mein Gedanke war zunächst den Def-Bereich zu
bestimnmen. Es können ansonsten Lösungen
herauskommen die gar nicht im Definitionsbereich
liegen.

Die Idee die Extremstellen über die 1.Ableitung
zu finden ist richtig.
Scheitert nur an der Komplexität der Formeln.

Dann kam bei mir die Überlegung : die Extremstellen
liegen auch dort wo die Extremstellen der
Zählerfunktion sin (4x) sind.
Dies stimmt aber nicht.

Eine einfache Lösung habe ich noch nicht
gefunden. Mit Newton und CAS ist dies möglich.

---

Vielen Dank für die Hilfe. Die Aufgabe ist aus einer Altklausur für: Mathematik für Chemiker. 

Da die Aufgabe nur 2 Punkte eingebracht hätte schätze ich das es sich hierbei um einen Fehler in der Aufgabenstellung handelt. Ans Newton verfahren habe ich auch gedacht habe mich aber entschieden die Funktion als ein Taylerpolynom darzustellen. 

---

Hilfsmittel sind keine erlaubt gewesen.

---

Die erste Ableitung ist nach meinem
Matheprogramm

 

3 Summanden.
im 2.Summanden kann sin (4x) ersetzt werden durch
cos(4x) * tan(4x)

Damit hat man in allen 3 Summanden den Faktor cos(4x)
der ausgeklammert werden kann.

Der Bruch ist dann 0 wenn der Zähler 0 ist.
Der Zähler ist null wenn cos(4x) = 0 ist

x = π / 8 + k / 4 * π

1.Nullstelle im positiven

x = π / 8

Hätten wir es damit ?

mfg Georg

---

Offensichtlich doch nicht.
x = 0.144 wäre das erste Maximum.

Siehst du bei mir einen Fehler ?

---

Hallo Georg,

sin(4x) = cos(4x) * tan(4x) 

gilt  nicht  für   cos(4x) = 0  (z.B. x = π/8)   ,  weil tan(4x)  für π/8  nicht definiert ist .

Gruß Wolfgang

---

Gut. Schön erkannt.