Interessanterweise kommen die definierenden Identitäten bei dieser Aufstelllung zum Logarithmus gar nicht vor:
https://www.matheretter.de/wiki/logarithmus#gesetze
Logarithmieren und Potenzieren hängen zusammen.
Betrachte die Definition im Link.
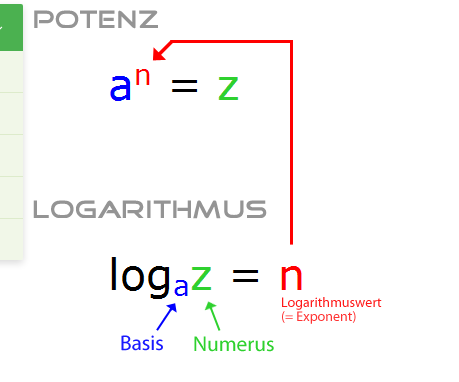
Setze das n oben bei Potenz ein:
Nun hast du die Identität
a ^ ( log_(a)(z)) = z , für z>0. Ergänzung ist nötig, damit der Logarithmus auch definiert ist. Ausserdem a>0.
a darf e sein.
e ^ log_(e)(z)) = z
Also:
e^ (ln(z)) = z