Untersuchen Sie die folgenden uneigentlichen Integrale auf Konvergenz: ∫_{0}^{1} 1/x - 1/sin(x) dx

Question

Untersuchen Sie die folgenden uneigentlichen Integrale auf Konvergenz:

$$\int _{ 0 }^{ 1 }{ \frac { 1 }{ x }  } -\frac { 1 }{ sin(x) } dx$$

uneigentlich weil ich ja keine 0 einstezen kann, da 1/0 nicht definiert ist.

Comments

ist die Aufgabe schon fertig?

Die Aufgabe ist fast fertig, wenn du den Grenzwert ausrechnen kannst, den Gast jc2144 in seiner Antwort vorgeschlagen hat. Grund: Im fraglichen Intervall ist f(x) =  (1/x - 1/sin(x)) nur für x=0  nicht definiert. 

Das sollte funktionieren: 

Graph des Integranden: https://www.wolframalpha.com/input/?i=(1%2Fx+-+1%2Fsin(x)) 

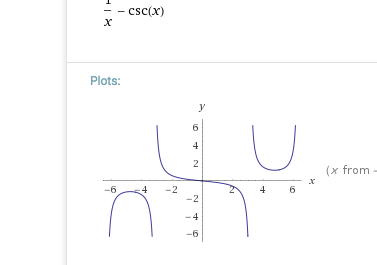
Ausserdem solltest du dann noch erwähnen, dass der Integrand f(x) =  (1/x - 1/sin(x))  im betrachteten Intervall stetig und überall definiert ist. Dann weisst du, dass der Integrand im angegebenen Intervall beschränkt ist. 

Sei nun S eine obere Schranke von |f(x)| 

==> Der Betrag des fraglichen Integrals ist kleiner oder gleich (Maximale Abweichung von 0)*(Intervallbreite)  =  S * 1 = S

lim (1/x - 1/sin(x))     | Bruchsubtraktion

= lim ((sin(x)-x)/(xsin(x)) 

.....  ? vielleicht klappt es mit 2 fach Hospital? 

Answer 1

zeige, dass

$$ \lim_{x\to0}\frac { 1 }{ x }-\frac { 1 }{ sin(x) }=0 $$

Die Funktion ist somit beschränkt und stetig auf [0,1], daher existiert dass uneigentliche Integral.

Comments

Also das ist ja klar... aber wie komm ich auf die konvergenz?

---

sollte ich das erstmal integrieren?

also 1/0 dx von 0 bis 1 für sich und - arcsin(x) von 0 bis 1 für sich?

und dann obere - untere grenze und dann ich das ergebnis die Lösung?

---

Satz: Eine beschänkte stetige Funktion f : [a, b] → R ist integrierbar.

Das Integral brauchst du nicht auszurechnen, der Wert ist nicht gefragt.

---

ok also ich hab soweit:

$$\int _{ 0 }^{ 1 }{ \frac { 1 }{ x } dx-\int _{ 0 }^{ 1 }{ arcsin(x)dx }  } = \int _{ r}^{ 1 }{ \frac { 1 }{ x } dx-\int _{ r}^{ 1 }{ arcsin(x)dx }  } $$

$$={ \left[ ln(x) \right]  }_{ r }^{ 1 }-{ \left[ ln(arcsin(x)+cot(x) \right]  }_{ r }^{ 1 }$$

was nun?

---

hmm.. egal hatte ich schon gemacht (hab ca eine stunde gebraucht)... xD

---

ist die Aufgabe schon fertig?

---

Wenn Du begruenden kannst, warum $$\lim_{a\to0+}\int_a^1\left(\frac{1}{x}-\frac{1}{\sin x}\right)\,dx$$ existiert, dann schon.