In einem Gefäß befinden sich drei schwarze und drei weiße Kugeln. Es werden nacheinander zwei Kugeln gezogen, wobei die erste Kugel nicht zurückgelegt wird.
Die Ereignisse
A: die erste Kugel ist schwarz und
B: die zweite Kugel ist weiß, sollen auf Unabhängigkeit untersucht werden.
a) Stellen Sie die Situation in einem Baumdiagramm dar.
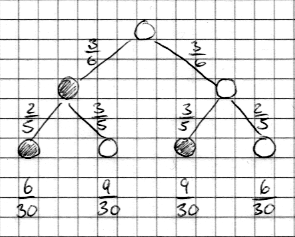
b) Berechnen Sie Pa(B) und Pb(A).
Pa(B) = P(A∩B) / P(A) = 9/30 / (3/6) = 3/5
Eigentlich kann man das ja auch direkt am Baumdiagramm ablesen.
Pb(A) = P(A∩B) / P(B) = P(A∩B) / ((P(A∩B) + P(-A∩B)) = 9/30 / (9/30 + 6/30) = 3/5
d) Begründen Sie die Abhängigkeit der Ereignisse A und B auf möglichst vielen Wegen.
Ein Weg ist das direkt oben aus dem Baumdiagramm abzulesen. Die Wahrscheinlichkeit von B hängt ja unmittelbar davon ab ob A eingetreten war oder nicht.
Ein anderer Weg führt über die Formel für die stochastische Unabhängigkeit
P(A) * P(B) = P(A∩B)
P(A) * P(B) = P(A) * ((P(A∩B) + P(-A∩B)) = 3/6 * (9/30 + 6/30) = 1/4 ≠ P(A∩B) = 9/30
Das ist hier also nicht erfüllt.