Brauche Hilfe bei folgenden Formeln: f(x)=2x³-2x u. g(x)=6/x²

Question

Wie bestimme ich die Funktionswerte an den Stellen 2 u. 3?

Wie bestimme ich die Definitionsmenge?

Wie sieht die Wertetabelle und der Graph aus?

Stehe im Moment völlig auf dem Schlauch.

Danke

Comments

also das was ich schätzen würde ist 0 0 12 48 120 aber wenn ich eine tabelle online erstelle kommt da was ganze anderes raus

Answer 1

1)

f(x)=2*x^3+2*x und g(x)=6/x^2

f(2)=2*2^3+2*2=36 und g(2)=6/4=3/2

f(3)=2*3^3+2*3=60 und g(3)=6/9=2/3

 

2) Definitionsmenge ist bei f(x) ganz R

bei g(x) R ohne 0 , also R\{0}

3)

 

Bei der Wertetabelle setzt du einfach so wie bei Punkt 1) ein paar beliebige Werte ein und schreibst die Funktionswerte hinzu.

Also z.b für f: 1 |0 und 2|36 und 3|60

Answer 2

Hi, 

Einsetzen ist die halbe Mathematik :-D

f(2) = 2 * 2³ - 2 * 2 = 16 - 3 = 12

f(3) = 2 * 3³ - 2 * 3 = 54 - 6 = 48

g(2) = 6 / 2² = 6 / 4 = 3/2 = 1,5

g(3) = 6 / 3² = 6 / 9 = 2/3

Die Definitionsmenge für f(x) ist die Menge der reellen Zahlen, man kann alles einsetzen. 

Bei der Definitionsmenge für g(x) muss man darauf achten, dass im Nenner eines Bruchs keine 0 stehen darf; deshalb ist die Definitionsmenge die Menge der reellen Zahlen ohne 0.

Eine Wertetabelle stellst Du so auf, dass Du mehrere Werte für x nimmst und dann f(x) bzw. g(x) ausrechnest wie oben vorgemacht. 

Wir hätten also jetzt schon eine Mini-Wertetabelle für f(x):

x       f(x)

2      12

3      48

Und eine Mini-Wertetabelle für g(x):

x    g(x)

2   1,5

3   2/3

Um den Graphen für z.B. f(x) zu erstellen, gehst Du vom Ursprung (0|0) x Stellen zur Seite und dann y Stellen nach oben oder unten, um einen Punkt einzuzeichnen. 

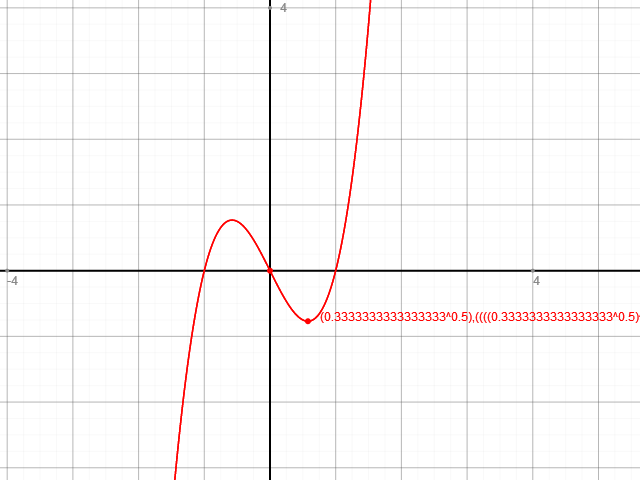
Der Graph von f(x) sieht so aus: 

Und der für g(x):

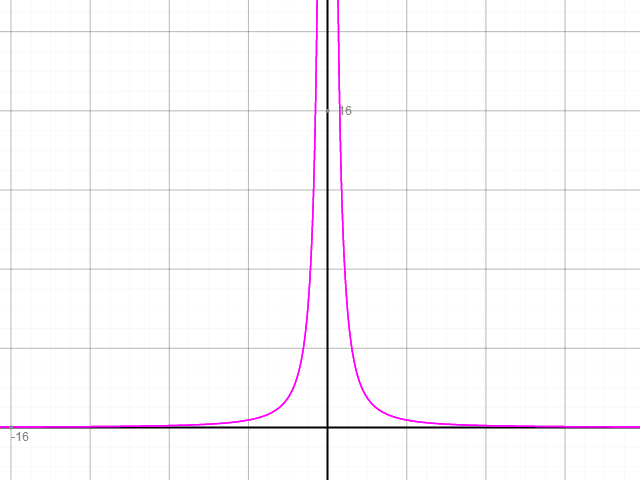
Besten Gruß

Comments

wenn x 2 ist und f(x) 12 wie kann der erste punkt dann so weit vorne sein??

---

Achte bitte auf den Maßstab des Graphen!

f(2) = 12, also der Punkt (2|12) ist hier ja gar nicht mehr eingezeichnet, weil wir als maximalen y-Wert in dieser Darstellung ja nur etwas mehr als 4 haben. 

Und der eingezeichnete Punkt im Graphen ist ein lokales Minimum, was sich wie folgt berechnet: 

f(x) = 2x³ - 2x

f'(x) = 6x² - 2 | die 1. Ableitung gibt die Steigung von f(x) in allen Punkten an. 

Damit wir ein Minimum haben, muss die 1. Ableitung = 0 sein und die 2. Ableitung > 0.

f'(x) = 6x² - 2 = 0

6x² = 2

x² = 1/3

x_1,2 = ± √(1/3)

f''(x) = 12x

f''(+ √(1/3)) = 12 * √(1/3) > 0, deshalb ein Minimum an der Stelle [√(1/3) | f(√(1/3))]

Analog ein Maximum an der Stelle [-√(1/3) | f(-√(1/3))]