Flugkurve eines Balls. f(x) = -0.135(x-10)^2 + 25. Quadratische Funktionen

Question

Aufgabe:

Max wirft einen Ball. Die Flugkurve kann durch folgende Gleichung  beschrieben werden: f(x)= -0,135(x-10)²+15

a. Nach wie vielen Metern hat der Ball seinen höchsten Punkt erreicht?

b. Welche Höhe hat der Ball an dieser Stelle?

c. Nach wie vielen Metern landet der Ball wieder auf dem Boden?

d. In welcher Höhe verlässt der Ball Max‘ Hand?

Comments

zu a und b: Die Koordinaten des Scheitels der Flugbahn sind die Lösungen.

zu c: die positive Nullstelle der Flugbahnfunktion ist die Lösung.

zu d: In der Höhe f(0) = ...

~plot~ -0,135*(x-10)^2+15; [[-1|22|-1|16]] ~plot~

Answer 1

Hallo HH,

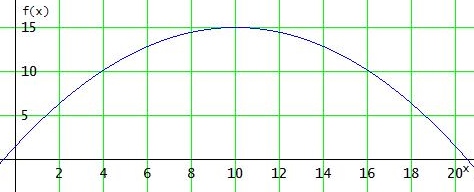
f(x)  =  - 0,135 · (x -10)²  + 15

 [ ich gehe mal von der nicht angegebenen Einheit Meter aus ]

x ist die (waagrechte) Entfernung vom Abwurfpunkt, f(x) die Wurfhöhe an der Stelle x

a)

f(x) stellt die Scheitelpunktform einer Parabel mit dem Hochpunkt (10 | 15 ) dar.

dieser Hochpunkt wird also nach 10 m erreicht

b)

die maximale Höhe ist also 15 m  

c)

Es muss  f(x) = 0 gelten:

 - 0,135 · (x -10)²  + 15  = 0  | -15

- 0,135 · (x -10)²  =  - 15  |  : (-0,135)

 (x -10)²   ≈  111,11   |  √

  x - 10  ≈  ±  10,54   | +10

x ≈  20,54  [ m ]   Auftreffpunkt nach 20,54 m   (die negative Lösung macht keinen Sinn)

d)  

Soll wohl "...Max' Hand "  heißen:

Beim Verlassen der Hand ist x = 0

Die gesuchte Höhe ist dann

f(0) = - 0,135 · (0 -10)²  + 15 =  1,5  [m]  

Gruß Wolfgang

Answer 2

a) Wir suchen an welche Stelle die Funktion das Maximum erreicht. Wir berechnen dazu die Nullstelle der ersten Ableitung.

In diesem Fall ist die Funktion Scheitelpunktform $$f(x)=a(x-d)^2+e$$ Davon bekommen wir dass die Koordinaten des Scheitelpunktes (höchste bzw. tiefste Punkt der Parabel) S(d | e) sind.

b) Wir berechnen das Maximum der Funktion.

Von den Koordinaten des Scheitelpunktes haben wir bereits das Maximum der Funktion. Es ist das e.

c) Wir wollen das x berechnen sodass f(x)=0.

d) Max wirft den Ball bei x=0. Die Höhe ist y-Koordinate. Wir wollen also das y=f(0) berechnen.

Comments

Die Art der Aufgabenstellung legt nahe dass b) nicht gelöst wird indem das Maximum bestimmt wird sondern der Scheitelpunkt.

Answer 3

Die Funktion liegt schon in der Scheitelpunktform
vor. Deshalb ergibt sich

a.) x = 10 m
b.)  max höhe = 15 m
c.)  f ( x ) = -0.135 * ( x - 10)^2 + 15  = 0
x = 20.54 m
d.) f ( 0 ) = -0.135 * ( 0 - 10)^2 + 15 = 1.5 m

Bei Bedarf nachfragen.