Für welche reellen Zahlen a ist die Funktion 4x^2-2axy+y^2 konvex?

Question

Rechenweg:

Für welche Reellen Zahlen a ist die Funktion 4x²-2axy+y² konvex??

 

danke für die hilfe!

Answer 1

Eine Funktion f ( x, y ) ist genau dann konvex bzw. streng konvex, wenn ihre Hesse-Matrix (also die Matrix der zweiten Ableitungen von f ) positiv semidefinit bzw. positiv definit ist.  

Die Hesse-Matrix von f ( x , y ) = 4 x ² - 2 a x y + y ² ist:

 

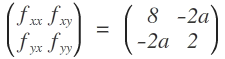
Sie ist positiv semidefinit, wenn gilt

1) f_xx ≥ 0 bzw. f_xx > 0 (vorliegend: f_xx = 8 > 0 , also erfüllt)

2) f_yy ≥ 0 bzw. f_xx > 0 (vorliegend: f_yy = 2 > 0 , also erfüllt)

3) f_xx * f_yy - ( f_xy) ² ≥ 0 bzw. f_xx * f_yy - ( f_xy) ² > 0

also vorliegend für den Fall der Semidefinitheit genau dann, wenn:

8 * 2 - ( - 2 a ) ² ≥ 0

<=> 16 ≥ 4 a ²

<=> - 2 ≤ a ≤ 2

Also:

Für { a ∈ R | - 2 ≤ a ≤ 2 } ist die Funktion f ( x , y ) = 4 x ²- 2 a x y + y ² konvex
Für { a ∈ R | - 2 < a < 2 } ist sie sogar streng konvex.