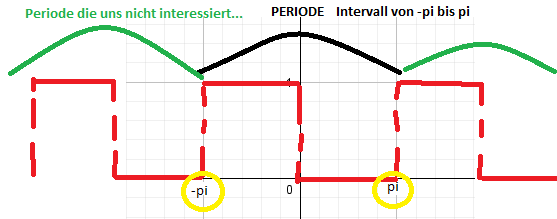
es handelt sich um eine 2 Pi Periodische Funktion!
Du musst herausfinden, ob es eine gerade oder ungerade Funktion ist, damit kann man sich dann einiges an Rechenarbeit sparen. Oft Sind Rechtecksfunktionen schön symmetrisch.
Berechnet werden kann aber auch ohne das Wissen über die Funktion dann sind a0 an und bn zu berechnen:
Kleiner Leitfaden: Ist eine Funktion gerade benötigt man "nur" a0 und an, ist sie ungerade nur bn
$$ { a }_{ 0 }=\frac { 1 }{ \pi } \int _{ -\pi }^{ \pi }{ f(x)dx } $$ Integralgrenzen bitte beachten!
$$ { a }_{ n }=\frac { 1 }{ \pi } \int _{ -\pi }^{ \pi }{ f(x)cos(nx)dx } $$
$$ { b }_{ n }=\frac { 1 }{ \pi } \int _{ -\pi }^{ \pi }{ f(x)sin(nx)dx } $$
Skizze kommt gleich: (Entschuldigung für das Gekrakel...)
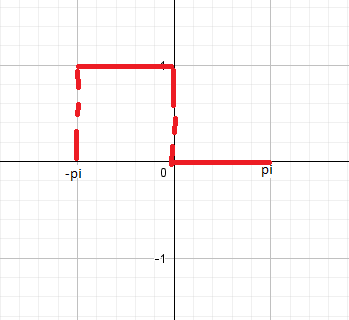
So Sieht dann deine Funktion aus! Bitte beim Integrieren die Grenzen beachten!
Wenn du dann deine a0 an und bn berechnet hast muss das in diese Allgemeine Formel eingesetzt werden:
$$ f(x)=\frac { { a }_{ 0 } }{ 2 } +\sum _{ n=1 }^{ inf }{ ({ a }_{ n }cos(nx)+{ b }_{ n }sin(nx)) } $$
Dann die ersten 3 Glieder berechnen (n = 1, n = 2, n= 3)...
Fertig!
Anmerkungen:
Lass dich bitte nicht von der 1 in der Skizze verunsichern, ich brauchte gerade nur ein Koordinatensystem ;-)
Skizzen helfen erstmal die Funktion zu verstehen, die sollte man sich immer zeichnen.
Es gibt auch T Periodische Funktionen, dann sehen die Integrale etwas anders aus!
Erweiterte Skizze: