32b)
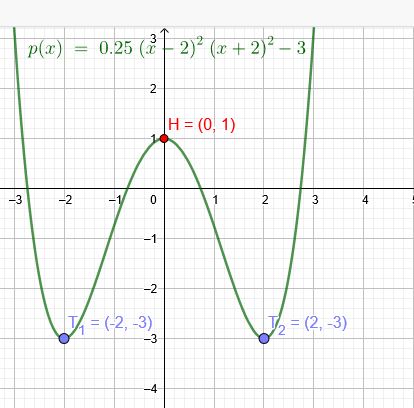
1.Tiefpunkt bei \( T_1(-2|-3)\)
verschieben um 3 Einheiten nach oben \( T´_1(-2|0)\)
2.Tiefpunkt bei \( T_2(2|-3)\)
verschieben um 3 Einheiten nach oben \( T´_2(-2|0)\)
Linearfaktorenfom:
\(f(x)=a(x-2)^2(x+2)^2\)
Hochpunkt bei H \((0|1)\)
verschieben um 3 Einheiten nach oben H´ \((0|4)\)
\(f(0)=a(0-2)^2(0+2)^2=16a=4\)
\(a=0,25\)
\(f(x)=0,25(x-2)^2(x+2)^2\)
verschieben um 3 Einheiten nach unten:
\(p(x)=0,25(x-2)^2(x+2)^2-3\)