Halbkugel Satz von Stokes.

Question

leider stehe ich total auf dem Schlauch.

$$\int_{F}^{} rot(V)N d\sigma$$ 

wobei N der Normalenvektor ist. Gilt nun weiterhin nicht etwa $$ d\sigma = \parallel F\left( u,v \right)_{ u } \times F\left( u,v \right)_{ v }\parallel d(u,v)$$$$ N = \frac{F\left( u,v \right)_{ u } \times F\left( u,v \right)_{ v }}{\parallel F\left( u,v \right)_{ u } \times F\left( u,v \right)_{ v }\parallel} $$

$$ d(u,v) = \parallel det'(u,v)\parallel du dv$$

Also folgt:

$$\int\int_{F}^{} rot(V)*(F\left( u,v \right)_{ u } \times F\left( u,v \right)_{ v })* \parallel det'(u,v)\parallel du dv$$ 

Hier die Aufgabenstellung:

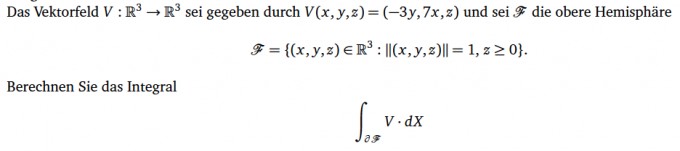
unter der Verwendung des Satzes von Stokes.

Irgendwie glaube ich meine "Herleitung/Umstellung" ist nicht korrekt. Ich bin momentan etwas verwirrt.... Vorallem der Normalenvektor N macht mir Probleme. 

Vielen Dank für die Hilfe.

Answer 1

hier die Herleitung des vektoriellen Flächenelements:

$$ \vec{ x }=\begin{pmatrix} rcos(\varphi)sin(\theta)\\rsin(\varphi)sin(\theta)\\rcos(\theta) \end{pmatrix}\\\vec{ x }_{\varphi}=\begin{pmatrix} -rsin(\varphi)sin(\theta)\\rcos(\varphi)sin(\theta)\\0 \end{pmatrix}\\\vec{ x }_{\theta}=\begin{pmatrix} rcos(\varphi)cos(\theta)\\rsin(\varphi)cos(\theta)\\-rsin(\theta) \end{pmatrix}\\d\vec{ A }=(\vec{ x }_{\varphi} \times \vec{ x }_{\theta})d\phi d\theta= \begin{pmatrix} -rsin(\varphi)sin(\theta)\\rcos(\varphi)sin(\theta)\\0 \end{pmatrix} \times \begin{pmatrix} rcos(\varphi)cos(\theta)\\rsin(\varphi)cos(\theta)\\-rsin(\theta) \end{pmatrix} d\phi d\theta\\=r^2 sin(\theta) \begin{pmatrix} -sin(\varphi)\\cos(\varphi)\\0 \end{pmatrix} \times \begin{pmatrix} cos(\varphi)cos(\theta)\\sin(\varphi)cos(\theta)\\-sin(\theta) \end{pmatrix}d\phi d\theta\\=r^2 sin(\theta)\begin{pmatrix} -cos(\varphi)sin(\theta)\\-sin(\varphi)sin(\theta)\\-cos(\theta) \end{pmatrix}\\=(-)r^2sin(\theta)\vec{ e }_{r}\\-> \vec{ n }=\vec{ e }_{r}\\dA=r^2sin(\theta) $$

(Das Minuszeichen ist bedingt durch die Reihenfolge im Kreuzprodukt und wird weggelassen, da per Konvention

der Normalenvektor nach außen zeigt. )

Comments

 

wir haben doch aber

$$ d\sigma $$ und nicht $$ d\vec{ \sigma }$$

? Ich sehe, es gibt scheinbar eine Beziehung welche lautet (was auch erklärt wo die Funktionaldeterminante hinverschwindet.. die suche ich schon die ganze Zeit):

$$ d\vec{ \sigma } = \vec{n} d\sigma = (F_{ u } \times F_{v}) du dv $$

also folgt 

$$ \int_{F}^{} rot(V)*\vec{n} d\sigma =\int \int rot(V)*(F_{ u } \times F_{v}) du dv   $$

mit $$ rot(V) = (0,0,10) $$ und

$$(F_{ u } \times F_{v}) = sin(\theta)\begin{pmatrix} cos(\varphi)sin(\theta)\\sin(\varphi)sin(\theta)\\cos(\theta) \end{pmatrix} $$

ist das Ergebnis

$$\int \int (0,0,10)*sin(\theta)\begin{pmatrix} cos(\varphi)sin(\theta)\\sin(\varphi)sin(\theta)\\cos(\theta) \end{pmatrix} du dv$$

Ich denke das stimmt so? Jedoch verstehe ich ich nicht was mit der Funktionaldeterminante passiert. Ich dachte die kommt immer dazu wenn man von d(u,v) zu dudv geht (Substitutionsregel)

---

Ja passt so, aber in der letzten Zeile heißt es am Ende dφdΘ anstatt dudv.

Außerdem fehlen noch die Grenzen.

Die Herleitung mit dem Kreuzprodukt entspricht der geometrischen Herleitung, da kommt die Funktionaldeterminate als Faktor "nebenbei" mit heraus.

https://de.wikipedia.org/wiki/Oberfl%C3%A4chenintegral#Oberfl.C3.A4chenelement

Man kann die Differentiale auch mithilfe des Transformationssatz berechnen, da berechnet man die Funktionaldeterminate explizit.

https://de.wikipedia.org/wiki/Transformationssatz

Das hängt damit zusammen, dass man Kreuzprodukte auch mithilfe von Determinanten berechnen kann.

$$ \vec{ a }\times \vec{ b }=|\begin{pmatrix}  \vec{ e }_{x} & \vec{ e }_{y} &\vec{ e }_{z} \\ { a }_{ x } & { a }_{ y }&{ a }_{ z }\\{ b }_{ x } & { b }_{ y }&{ b }_{ z } \end{pmatrix}| $$

---

wie kann es denn sein dass 

$$ \int_{F}^{}1* d\vec{\sigma} = \int \int_{}^{}\parallel F_{ \varphi } \times F_{\theta} \parallel d\varphi d\theta $$

schon einmal vielen Dank.

---

Nee so ist es verkehrt, links steht ein Vektor unter dem Integral  und rechts steht nur eine Zahl wegen dem Betrag. Richtig lautet es

$$  d\vec{\sigma} =  (F_{ \varphi } \times F_{\theta})  d\varphi d\theta $$so wie bei dem Wiki-Link.

---

Ich komme darauf, da 

Unter Verwendung der Zylinderkoord. und oben beschriebenen "falschen" Zusammenhang komme ich auch auf das richtige Ergebnis.... (ja die Aufgabe hatte ich schon gepostet, aber mir fällt gerade auf das ich einen falschen Zusammenhang gewählt habe :D)

Edit: Entweder verstehe ich jetzt gar nichts mehr, oder dass ist falsch beschriftet...