Kurvendiskussion f(t) =e-t*sint

Question

Man bestimmte für die Funktion:

f(t) =e^{-t}*sint   (t>=0)

a) Nullstellen,
b) Extremwerte (Maxima und Minima),
c) Wendepunkte,
d) Schnittpunkt mit der Ordinatenachse,
e) Verhalten für betragsmäßig große Argumentwerte,
f) zu (2): Schnittpunkte (Berührpunkte ?) mit der Einhüllenden,

Answer 1

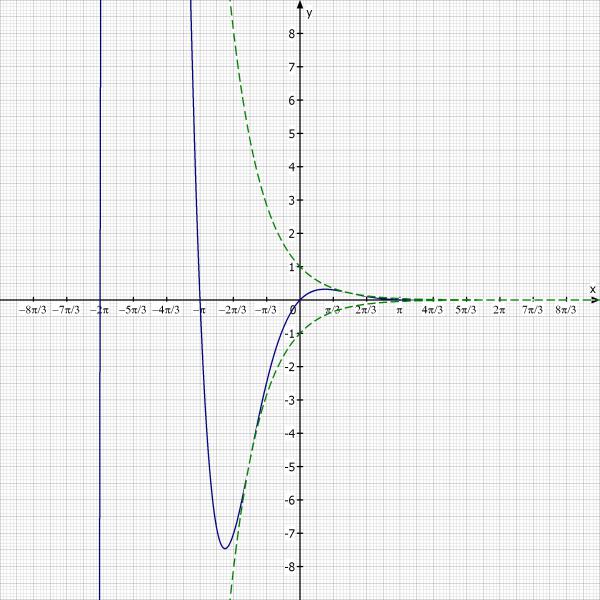
Funktionsgleichung
f(x)=e^-x*sin(x)

1. Ableitung
f'(x)=-e^-x*(sin(x)-cos(x))

2. Ableitung
f''(x)=-2*e^-x*cos(x)

3. Ableitung
f'''(x)=2*e^-x*(sin(x)+cos(x))

a) Nullstellen bei
x =-9,4247, x =-6,2831, x =-3,1415, x =3,1415, x =6,2831, x =9,4247, x =0

b) Extremstellen
x = pi/4 + k·2·pi
x = 5/4·pi + k·2·pi

EP1(pi/4 + k·2·pi, f(pi/4 + k·2·pi))
EP2(5/4·pi + k·2·pi, f(5/4·pi + k·2·pi))

c) Wendepunkte
Wendepunkt bei ( pi/2 | 0,2078 )

 

d) f(0) = 1

e) Grenzwert gegen plus unendlich lim_(x->oo) f(x)=0
Waagrechte Asymptote bei y = 0

Grenzwert gegen minus unendlich
lim_(x->-oo) f(x)=existiert nicht

 

f) e^-x·SIN(x) = ± e^-x

SIN(x) = 1

x = pi/2 + k·2·pi und x = 5/2·pi + k·2·pi

SIN(x) = -1

x = - pi/2 + k·2·pi und x = - 5/2·pi + k·2·pi

Skizze: