Hallo bobomo,
Zunächst gilt es zu erkennen, dass in der Skizze mehrere ähnliche rechtwinklige Dreiecke enthalten sind.
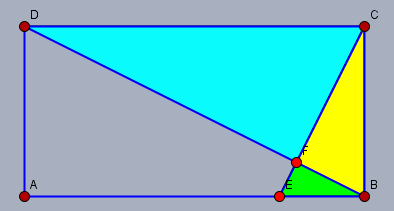
Ich habe Dir das grüne, das gelbe und das hellblaue mal markiert. 'ähnlich' bedeutet, dass alle WInkel in diesen Dreiecken gleich sind und alle Strecken untereinander in einem festen Verhältnis stehen. Ich betrachte jetzt nur die Katheten der Dreiecke.
Es existiert (ein zunächst unbekannter) Faktor \(f\) mit dem man die kürzere Kathete multipliziert und die längere erhält. Also im gelben Dreieck
$$FC = f \cdot FB$$
Das muss im hellblauen genauso gelten (da ähnlich!)
$$DF = f \cdot FC$$
\(DF\) ist aber laut Aufgabestellung \(DF=4 \cdot FB\) und \(FC = f \cdot FB\) - einsetzten ergibt dann
$$4 \cdot FB = f \cdot f \cdot FB = f^2 \cdot FB \quad \Rightarrow \space f=2$$
D.h. jede lange Kathete ist genau doppelt so lang, wie die kürzere. Also ist
$$FB = 2 \cdot EF = 4 \text{cm}$$
$$FC = 2 \cdot FB = 8\text{cm}$$
Auch das Dreieck \(BCD\) ist ähnlich zu den farblich markierten. Demnach gilt auch hier das gleiche Kathetenverhältnis
$$CD = 2 \cdot BC$$
Die Fläche \(A\) des Rechtecks \(ABCD\) ist Breite mal Höhe - also:
$$A = CD \cdot 2 \cdot BC = 2 \cdot |BC|^2$$
Um \(|BC|^2\) zu berechnen betrachte ich das Dreieck \(EBC\). Nach Pythagoras gilt:
$$|BC|^2 = |EC|^2 - |EB|^2 = (EF + FC)^2 - (|EF|^2 + | FB|^2)$$ $$\space= \left( 2\text{cm} + 8\text{cm}\right)^2 - \left( (2\text{cm})^2 + (4\text{cm})^2\right)= 80\text{cm}^2$$
Also ist
$$A= 2 \cdot |BC|^2 = 160\text{cm}^2$$