Ich soll zeigen, dass die Keplersche Fassregel für das folgende Integral den exakten Wert liefert. Den Integral habe ich bereits bestimmt, aber ohne die Kapplersche Regel. Heraus kommt 4/3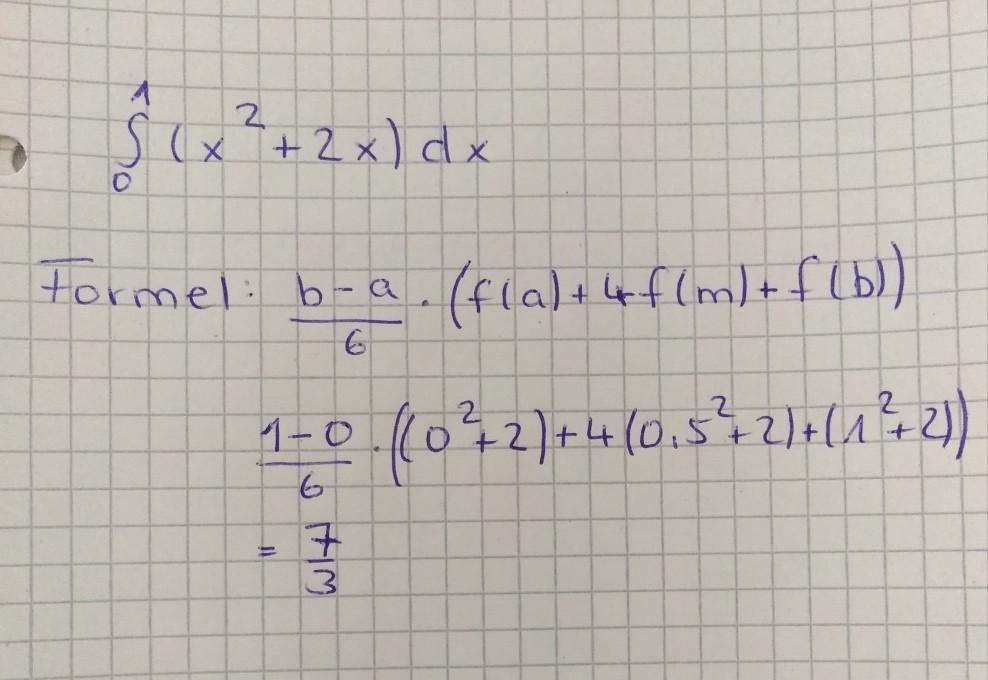 . Nun weiß ich nicht genau, wie ich das mit der Fassregel machen soll.
. Nun weiß ich nicht genau, wie ich das mit der Fassregel machen soll.
Ich habe es bisher versucht zu berechen, komme aber nie auf 4/3.
Freue mich auf Antworten. :)