Dreieck mit Ecken auf Parabel maximieren

Question

folgende Aufgabe könnte ich auch selber lösen. Ich brauche das ganze aber 'öffentlich' im I-Net, da ein Freund von mir die Antwort für seinen Mathe-Unterricht benötigt.

Es seien zwei Punkte $A$ und $B$ auf einer Parabel $y=x^2$ gegeben. Es ist ein dritter Punkt $C$ auf der Parabel gesucht, dessen X-Koordinate sich im Intervall $(a_x .. b_x)$ befindet und der so liegt, dass die Fläche des Dreiecks $ABC$ ein lokales Maximum hat.

Tobt Euch aus ;-) ... umso mehr unterschiedliche Lösungen, desto besser.

Gruß Werner

Comments

Ich werde die Antworten noch kommentieren und die Rechenwege ausführen. Damit ich die Bezeichner nicht jedes mal neu hinschreiben muss - hier die Definitionen:

Die Koordinaten von $A$ seien $(a_x;a_y)$, die von $B$ $(b_x;b_y)$ und $C$ entsprechend $(c_x;c_y)$ mit $c_y=f(c_x)={c_x}^2$

Außerdem führe ich noch die Größe $m$ ein - mit

$$m=\frac{b_y-a_y}{b_x-a_x}$$

was im Falle von $b_x > a_x$ der Steigung der Geraden durch $A$ und $B$ entspricht.

Alles weitere folgt als Kommentar hinter der jeweiligen Antwort.

Answer 1

Hallo Werner,

falls dies der Sachverhalt ist.

Bestimme die Steigung der Geraden AB.
Setze in die erste Ableitung f ´( x ) = 2x
2x = m (AB) ein.
xc ist die Stelle mit dem größten Abstand von AB
und damit ist das Dreieck ABC mit dem
größten Flächeninhalt gefunden.

Comments

Deine Frage / Antwort und den Stern von dir werde ich
ausschneiden und mir überm Bett aufhängen. ;-)

PS. Die Frage hatten wir im Forum schon
einmal.

---

Wenn wir die Frage schon hatten, hast Du einen Link?

Meinst Du dies: https://www.mathelounge.de/404239/extremwertaufgabe-dreieck-unter-ei…

---

Ja. Fülltext.

---

Ja - und die Lösung von Georg ist IMHO die eleganteste. Es ist offensichtlich, dass ein Punkt $C$ auf der Parabel, sich nicht mehr weiter von der Geraden durch $AB$ entfernen lässt, wenn er im Berührpunkt der Tangenten liegt, die die gleiche Steigung $m$ wie die die Gerade durch $AB$ hat.

Ableiten der Funktion der Parabel ist

$$y'=2x$$

Mit der Bedingung, dass $y'=m$ für das optimale $C$ ist - erhält man

$$y'(c_x) = m = 2 c_x$$

Und daraus folgt natürlich

$$c_x= \frac{m}{2} = \frac{b_y - a_y}{2(b_x - a_x)} = \frac{b_x^2 - a_x^2}{2(b_x - a_x)}\\\phantom{c_x}=\frac{(b_x-a_x)(b_x+a_x)}{2(b_x - a_x)} = \frac{1}{2}(b_x+a_x)$$

Answer 2

Hier findest du eine Formel, wie es mit Vektoren geht:

https://de.serlo.org/mathe/geometrie/dreiecke-vierecke-kreise-andere…

Comments

Diese Lösung war die erste, die mir in den Sinn kam, als ich die Aufgabe sah. Die Fläche $F$ des Dreiecks lässt sich unmittelbar aus dem Kreuzprodukt (bzw. der Determinante) berechnen. Es ist:

$$F= \frac{1}{2} \vec{AC} \times \vec{AB}$$

Der Vektor $\vec{AB}$ sei ein Vielfaches von $(1;m)$ - also $$\vec{AB}=\begin{pmatrix} k \\ k \cdot m\end{pmatrix}$$

Dann ergibt sich

$$F = \frac{1}{2} \left( \begin{pmatrix} c_x - a_x\\ {c_x}^2 - a_y\end{pmatrix} \times \begin{pmatrix} k \\ k \cdot m\end{pmatrix} \right)$$

$$\space = \frac{1}{2} \left( ( c_x - a_x)km - ({c_x}^2 - a_y)k \right)$$

Das kann man schon nach $c_x$ ableiten

$$\frac{\partial F}{\partial c_x} = \frac{k}{2}(m - 2c_x) \quad \rightarrow 0$$

Daraus folgt dann

$$c_x=\frac{m}{2}= \frac{b_y - a_y}{2(b_x - a_x)}$$

Answer 3

Die Punkte sind A(a|a²), B(b|b²) und C(c|c²). Bestimme den Betrag g des Vektors von A nach B und den Abstand h des Punktes C von der Geraden AB. Dann ist die Fläche F des Dreiecks ABC: F=g·h/2. Damit daraus eine Funktionsgleichung wird, müsste geklärt werden,was bekannt und was unbekannt ist. 

Comments

Ich zitiere: "Es seien zwei Punkte $A$ und $B$ auf einer Parabel $y=x^2$ gegeben" Die Koordinaten von $A$ und $B$ sind gegeben. $C$ ist gesucht. Alle Punkte liegen auf der Parabel.

---

Der Betrag der Strecke $AB$ ist gegeben und daher konstant und spielt folglich für den Lösungsweg keine Rolle. Es reicht aus die Höhe $h_c$ - d.h. den Abstand des Punktes $C$ von der Geraden $g$ durch $A$ und $B$ zu maximieren.

Dazu bestimme ich die Geradengleichung in der Normalform. Aus folgender Überlegung ..

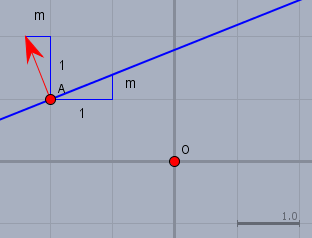
.. folgt, dass ein Normalenvektor $\vec{n}$ der Geraden

$$\vec{n} = \begin{pmatrix} -m\\ 1 \end{pmatrix}$$

ist. Damit und mit dem Punk $A$ stelle ich die Normalengleichung auf:

$$g: \space \vec{n} \cdot \vec{x} = \vec{n} \cdot \begin{pmatrix} a_x\\ a_y \end{pmatrix}=-m \cdot a_x + a_y$$

Ein Maß $h^*$ für den Abstand eines Punktes $C$ (mit Ortsvektor $\vec{c}$) ist

$$h^* = \vec{n} \cdot \vec{c} + m \cdot a_x - a_y$$

Wohlgemerkt ist $h^*$ nicht direkt der Abstand von $C$ von $g$, da ich $\vec{n}$ nicht normiert habe, aber es ist ein Vielfaches des Abstands und es reicht daher aus, diesen Wert zu maximieren. Einsetzten der Koordinaten von $C$ ergibt dann:

$$h^*(c_x) = -m\cdot c_x + {c_x}^2 + m \cdot a_x - a_y$$

und ableiten nach $c_x$

$$\frac{\partial h^*}{\partial c_x} = -m + 2c_x \quad \rightarrow 0$$

Und das Ergebnis ist dann

$$c_x = \frac{m}{2}= \frac{b_y - a_y}{2(b_x - a_x)}$$

Answer 4

eine weitere Möglichkeit mit Vektoren:

Berechne das Kreuzprodukt aus CA und CB . Der Betrag davon ist dann zu maximieren.

Comments

Danke für die Antwort - ist aber im Kern identisch mit der Antwort von Gast2016.

---

Oh ich hab aufgehört den Link weiterzuverfolgen als ich da "Artikel in Arbeit" gelesen habe :D