Flächeninhalt maximieren Dreieck

Question

Gegeben sein Kreis mit Radius R = 1, der seinen Mittelpunkt im Ursprung hat. Welches Dreieck, dessen Eckpunkte auf dem Kreis liegen, hat den größten Flächeninhalt? Begründen Sie Ihre Antwort.

Problem:

Wie komme ich hier weiter. Ich denke dass das Dreieck leichschenklig sein muss, aber wie beweise ich das?

Answer 1

Hallo Niklas,

zeichne ein beliebiges Dreieck in einen Kreis ein und durch einen der Eckpunkte eine Parallele zur gegenüber liegenden Seite (hier schwarz gestrichelt).

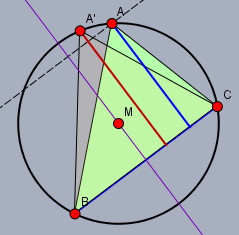
Der Flächeninhalt \(F\) des Dreiecks \(\triangle ABC\) berechnet sich aus der Grundseite \(BC\) und der Höhe \(h_c\) (blau)$$F = \frac 12 |BC| h_c$$wenn die Parallele den Kreis schneidet, existiert ein Punkt \(A'\) und damit das Dreieck \(\triangle A'BC\) mit der Höhe \(h_c'\) (rot) und einem Flächeninhalt \(F'\)$$F' = \frac 12 |BC| h'_c \gt  F', \quad h'_c \gt h_c$$Nur wenn \(A'\) auf der Mittelsenkrechten (lila) zu \(BC\) liegt, wäre die Fläche maximal. Weiter ist in diesem Fall \(|A'B| = |A'C|\).

Diese Betrachtung kann mann für jeden der drei Punkte wiederholen. Man erreicht also genau dann den größten Flächeninhalt, wenn alle Seiten paarweise gleich lang sind.

Daraus folgt: das Maximum an Fläche wird mit einem gleichseitigen Dreieck erreicht.

Comments

Okay, danke für die Begründung, Sie haben mir sehr geholfen. Doch wie rechne ich jetzt noch den Flächeninhalt aus?

---

Doch wie rechne ich jetzt noch den Flächeninhalt aus?

Ich gehe davon aus, dass der Radius \(r\) des Kreises gegeben ist. Im gleichseitigen Dreieck fallen die Höhen, die Mittelsenkrechten und die Seitenhalbierenden zusammen und damit auch der Höhenschnittpunkt und der Schwerpunkt. Da sich die Seitenhalbierenden in jedem Dreieck im Verhältnis 2:1 teilen, ist die Höhe $$\frac 23 h = r \implies h = \frac 32 r$$und weiter ist im gleichseitigen Dreieck in Abhängigkeit der Seite \(s\) (nach Pythagoras)$$\begin{aligned}h &= \frac 12 \sqrt 3\, s \\ \implies s &= \frac{2}{\sqrt 3} h = \sqrt 3 \, r \\ F &= \frac 12 hs \\&= \frac 12 \cdot \frac 32 r \cdot \sqrt 3\, r \\&= \frac 34 \sqrt 3 \,r^2\end{aligned}$$

---

Vielen Dank!!!

Answer 2

Nicht gleichschenklig sondern sogar gleichseitig.

Nimm die Strecke BC. Wo müsste der Punkt A liegen damit das Dreieck maximal wird? Über der Mittelsenkrechten der Strecke BC, weil dort die Höhe maximal wird.

Das heißt zu jeder Strecke müsste der Dritte punkt immer auf der Mittelsenkrechten liegen. Damit ist das Dreieck gleichseitig.

Comments

Und wie beweise ich, dass das Dreieck gleichseitig sein muss, damit der Flächeninhalt maximal wird?