Hallo noch einmal, Assyrianlove! :-)
a)
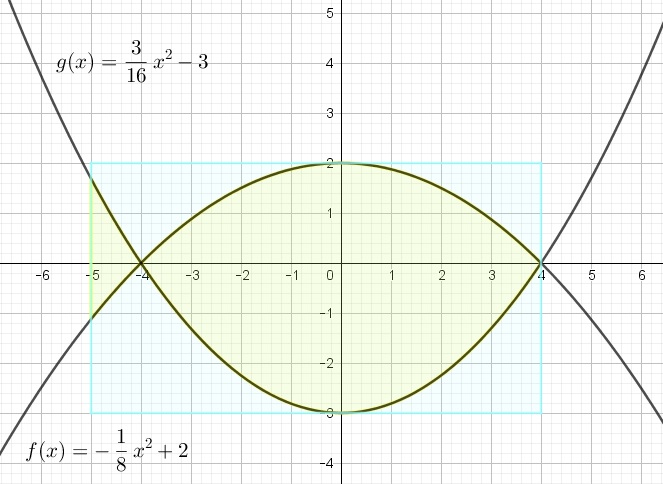
f(x) = -1/8 x^2 + 2
g(x) = 3/16 x^2 - 3
b)
A = 28,021 dm^2
(Siehe Rechnung unten.)
c)
AFisch / ARechteck = 28,021/54 = 0,52. Der Fisch bedeckt 52 % des Fensters.
Der Lichteinfall vermindert sich um 0,5 * 0,52 = 0,26 = 26 %
d) Hier sind eventuell mehrere Varianten möglich.
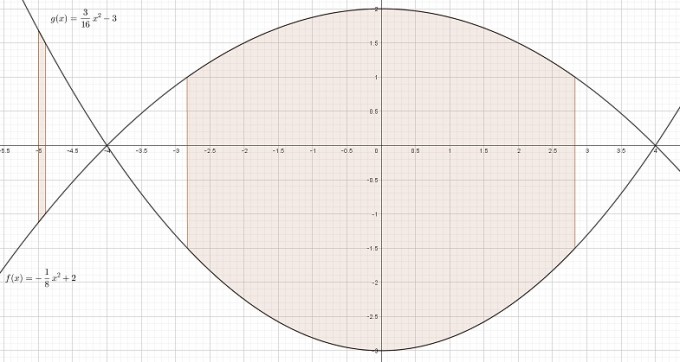
Bereich -4 < x < 4
g(x) < 0 -> |g(x)| = -g(x)
f(x) + |g(x)| = 2,5
-1/8 x^2 + 2 - 3/16 x^2 + 3 = 2,5
-5/16 x^2 + 5 = 2,5
x1,2 = ±√(8)
Im Bereich -√(8) <= x <= √(8) ist das Logo mindestens 25cm hoch.
Bereich -5 <= x < 4 (Heckflosse)
f(x) < 0 -> |f(x)| = -f(x)
|f(x)| + g(x) >= 2,5
1/8 x^2 - 2 + 3/16 x^2 - 3 = 2,5
5/16 x^2 = 7,5
x1,2 = ±√(24)
Im Bereich -5 <= x <= -√(24) ist das Logo mindestens 25cm hoch.
Berechnung des Flächeninhaltes:
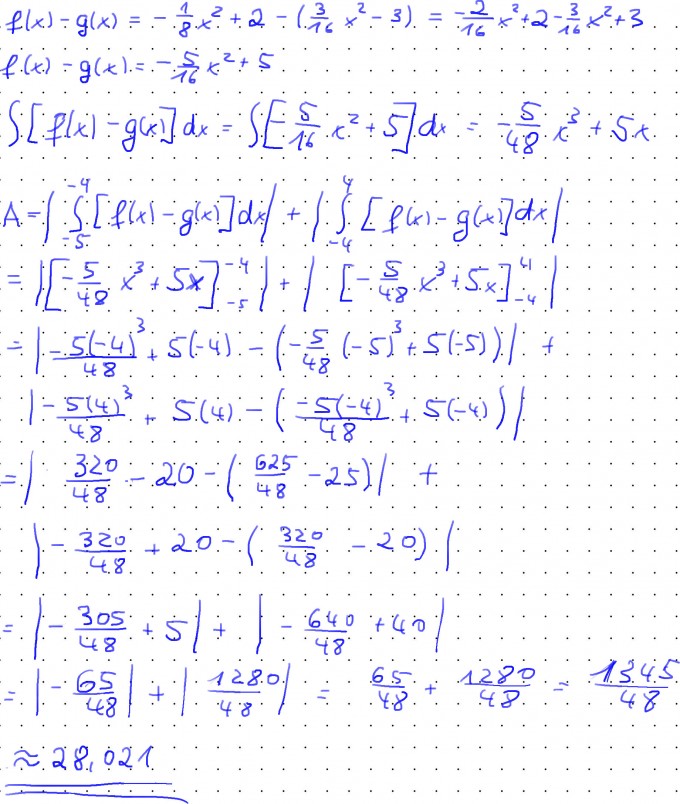
Beste Grüße
gorgar