Hallo Sanny,
ich versuche noch mal eine andere Erklärung. Dazu habe ich Dir die Funktion
$$y=(x-3)^2+1$$
in blau skizziert. In grün siehst Du die Funktion um +1 in Y-Richtung verschoben und in rot die Funktion um +1 in X-Richtung verschoben.
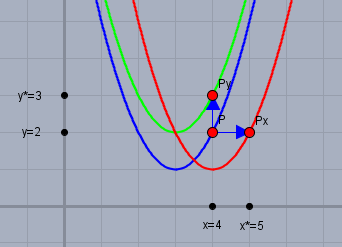
Wie kommt man jetzt zu den jeweils verschobenen Funktionen? dazu betrachte ich beispielhaft den Punkt \(P(4|2)\). Wenn ich den nach oben verschiebe, so muss ich die Y-Koordinate um 1 erhöhen, ich bekomme dann natürlich eine andere Funktion, weil ich auch ein anderes Y habe - das nenne ich mal \(y^*\). Es ist offensichtlich
$$y^*=y+1$$
Um jetzt die neue Funktion mit \(y^*\) zu erhalten, setze ich die Funktionsgleichung von oben hier ein, so dass das \(y\) heraus fällt.
$$y^*=y+1=\left((x-3)^2+1\right)+1=(x-3)^2+2$$Für die Verschiebung in X-Richtung wieder um +1 gehe ich nun genauso vor. Das neue X soll \(x^*\) heißen und genau wie beim Y gilt $$x^*=x+1$$Damit ich dies und die ursprüngliche Funktionsgleichung miteinander verknüpfen kann, so dass das X heraus fällt, stelle ich es zunächst um: \(x=x^*-1\) und setze es dann ein und erhalte
$$y=(x-3)^2+1=y=((x^*-1)-3)^2+1=(x^*-4)^2+1$$
Du siehst, dass in beiden Fällen (X und Y) das gleiche gemacht wird. Dass am Ende augenscheinlich das Vorzeichen einmal invertiert werden muss und einmal nicht, liegt nur an der Stellung von X bzw. Y innerhalb des Funktionsterms.
Gruß Werner