Grenzwerte: f(x) = 1/x + 1/(1+x) und g(x) = (2 - x) / (x^2 - 2x)

Question

Hey ich habn riesen problem ich verstehe die berechnung von grenzwerten nicht :/ Hab im internet immer schon nach anleitungen geguckt aber da wie das dabei was ich brauch...

Kann mir jemand das an den beiden beispielen erklären?

f(x) = 1/x + 1/(1+x) und
g(x) = (2 - x) / (x^2 - 2x)

Also für den Def. Bereich muss man ja die zahl nehmen wenns im nenner 0 steht.

So aber ich versteh nich genau die termumformung und die h methode . Wie wären die grenzwerte wenn x gegen unendlich und x0 strebt?

Schreib dienstag n test und kann auch kein aus meinem tutorium fragen weil das irgendwie keiner versteht :o

Comments

Du hast bisher noch keine Antwort erhalten, weil du die Schreibregeln nicht eingehalten hast. Wo fangen Zähler und Nenner an bzw. hören sie auf?

1 min schauen und du weißt, was gemeinst ist:

Answer 1

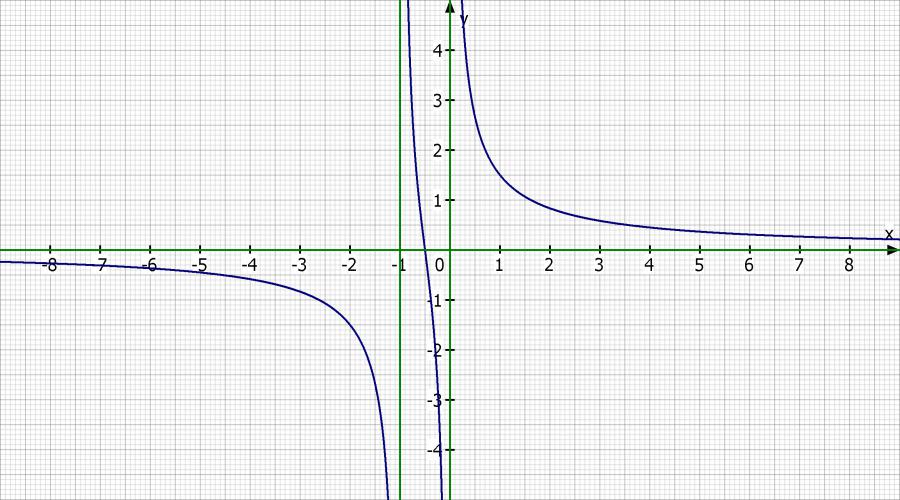
f(x) = 1/x + 1/(1+x)

lim (x→-∞) f(x) = -0

lim (x→∞) f(x) = 0

Ich hoffe das bereitet keine SchSchwierigkeiten 

Schwierig sind jetzt die Stellen 0 und -1 wo die Nenner 0 werden.

Jetzt setzt du einmal etwas minimal kleineres als 0 ein und einmal etwas minimal größeres als 0

lim (x→0-h) 1/(0-h) + 1/(1+(0-h)) = -∞ + 1 = -∞
lim (x→0+h) 1/(0+h) + 1/(1+(0+h)) = ∞ + 1 = ∞

Jetzt das gleiche mit -1

lim (x→-1-h) 1/(-1-h) + 1/(1+(-1-h)) = -1 - ∞ = -∞
lim (x→-1+h) 1/(-1+h) + 1/(1+(-1+h)) = -1 + ∞ = ∞

Skizze:

Comments

g(x) = (2 - x) / (x^2 - 2x)

g(x) = (2 - x) / (-x * (2 - x))

Ich mache hier jetzt eine stetige ergänzung indem ich durch (2 - x) kürze.

g(x) = 1 / (-x) = -1/x

Diese Funktion sollte jetzt eigentlich keine Probleme bereiten.

Sie gehört zu denen deren Verlauf man eh auswendig wissen sollte.