Hi,
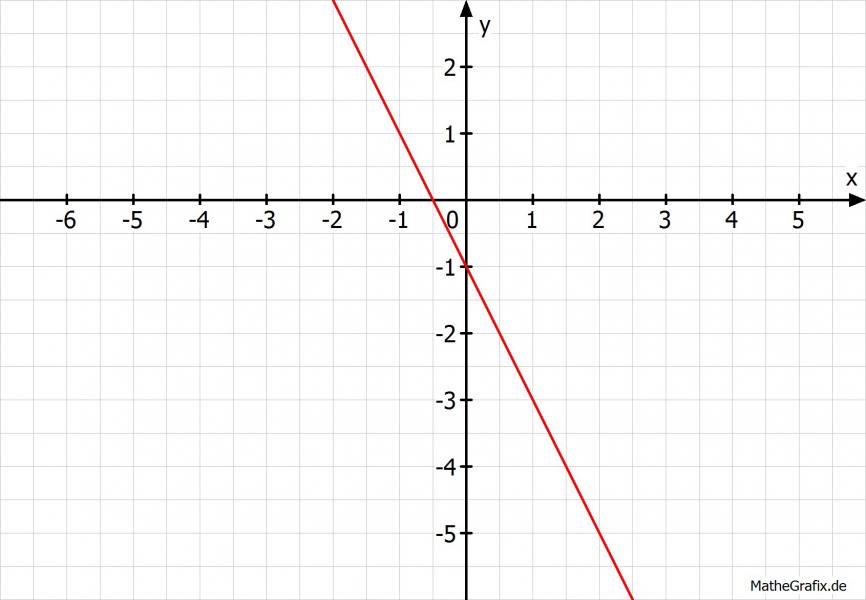
f(x) = -2x-1
Starte am besten beim y-Achsenabschnitt wie Du es schon gesagt hattest. Dieser gibt den Punkt an, wo die Gerade die y-Achse schneidet. Also bei P(0|-1). Dann nimm das Steigungsdreieck. Das bedeutet Du gehst von diesem Punkt P ein Schritt nach rechts. Dann gehe um so viele Schritte nach oben oder unten wie es angezeigt wird. Hier also zwei Schritte nach unten (nach unten, da negatives Vorzeichen).
In unserem Falle solltest Du dann bei Q(1|-3) rauskommen. Da sieht so aus:
Für g(x) = 2x-1 gehst Du genauso vor, doch gehe nun noch 2 nach unten, sondern 2 nach oben:
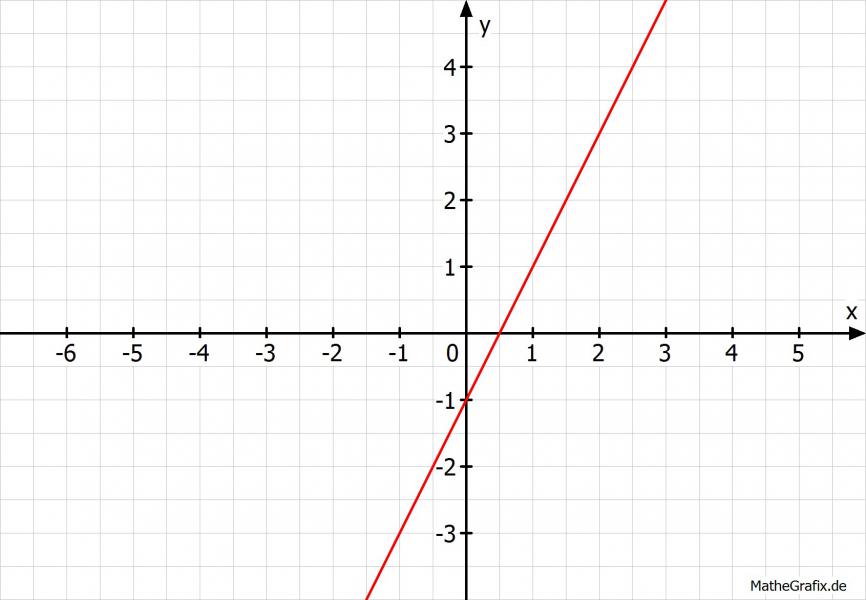
Alles klar?
Grüße