Hallo Andrei,
ich habe in der Skizze zwei (blaue) Geraden eingezeichnet.
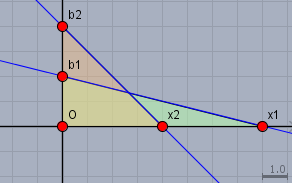
Die beiden Dreiecke \(OX_1B_1\) und \(OX_2B_2\) haben beide den Flächeninhalt von \(8\). Mal angenommen, ich wähle auf der Y-Achse den Wert \(b\), dann ist der Zusammenhang mit dem Schnittpunkt \(a=x_i\) der Geraden mit der X-Achse der zugehörigen Geraden
$$ \frac12b \cdot a = 8 \quad \Rightarrow a = \frac{16}{b}$$
Die zugehörige Geradengleichung ist allgemein \(y=mx+b\) mit \(b\) als Schnittpunkt mit der Y-Achse und die Steigung \(m\) ist:
$$m=\frac{-b}{a} = \frac{-b}{16/b}=\frac{-b^2}{16}$$
Somit ist die Gleichung für die Geradenschar in Abhängigkeit des Parameters \(b\):
$$y(x)=\frac{-b^2}{16} x + b$$
Gruß Werner