Weg mit Quadrieren:
Aufgabe 1:
\(|x+2|=2x-5\)
\(\sqrt{(x+2)^{2}}=2x-5 |^{2}\)
\((x+2)^{2}=(2x-5)^{2}\)
\((x+2)^{2}-(2x-5)^{2}=0\) 3.Binom:
\([(x+2)+(2x-5)]\cdot [(x+2)-(2x-5)]=0\)
\([3x-3]\cdot [-x+7]=0\) Satz vom Nullprodukt:
1.)
\(3x-3=0\)
\(x_1=1\) Probe, weil Quadrieren keine Äquivalenzumformung ist:
\(3=2-5\) Stimmt nicht
2.)
\(x_2=7\)
\(9=9\) ✓
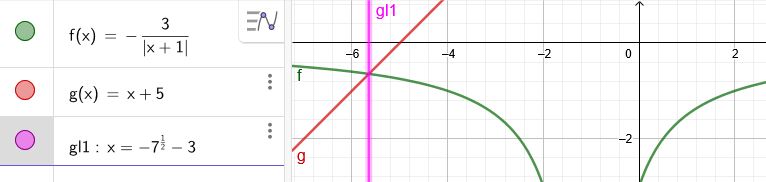
Aufgabe 2:
\( \frac{-3}{|x+1|}=x+5|^{2} \) mit \(x≠-1\)
\( \frac{9}{(x+1)^{2}}=(x+5) ^2 \)
\( 9=(x+5) ^{2}(x+1)^{2} \)
\((x^{2}+6x+5)^{2}=9 |±\sqrt{~~} \)
1.)
\(x^{2}+6x+5=3 \)
\(x^{2}+6x=-2 \)
\(x_1=\sqrt{7}-3 \)
\(x_2=-\sqrt{7}-3 \)
2.)
\(x^{2}+6x+5=-3 \)
\(x^{2}+6x=-8 \)
\(x_3=-4\)
\(x_4=-2\)
Auch hier wieder die Proben!