Abbildungseigenschaften injektiv, surjektiv oder bijektiv. Bsp. f:R-> R mit y= f (x) = x+lxl

Question

Hallo alle zusammen,

Ich bin ersti und komme gerade nicht mit der Mathematik Aufgabe zu recht. Es waere echt nett wenn mir jemand helfen koennte.

Aufgabe:

EDIT(gemäss Kommentar): Definitionsmengen und Wertebereiche gegeben mit f:R-> R mit y=f (x)

Sind die Funktionen injektiv,  surjektiv oder bijektiv? Begründen Sie ihre Antwort

1. y=x+lxl

2. y=4sin (2x-7)

3. (x-2)^2+(y+1)^2=4 mit y>= -1

4. y=x^2+2x+2

5. y=x^3

Comments

Sind Definitionsmengen und Wertebereiche denn angegeben? Die brauchst du bei jeder Funktion um das beurteilen zu können.

---

Ja, das ist gegeben mit f:R-> R mit y=f (x)

---

EDIT: Oben ergänzt und gleich noch dein Wort subjektiv durch surjektiv ersetzt. Das bedeutet, dass alle Werte im Wertebereich auch wirklich als Funktionswerte vorkommen. Bei a) dürfte das nun nicht der Fall sein, da ich keine Möglichkeit für eine negatives Resultat bei x+lxl sehe.

Answer 1

" f: R -> R mit y=f (x) "

Mit dieser Vorgabe ist die Aufgabe etwas langweilig. 

1. y=x+lxl , nicht surjektiv , nicht injektiv (f(-1) = f(-2) = 0), nicht bijektiv

2. y=4sin (2x-7), nicht surjektiv. Angenommen werden nur die Werte zwischen -4 und + 4 inkl. -4 und 4.

Nicht injektiv, da sin(0) = sin(π) = sin(2π)

==> nicht bijektiv.

3. (x-2)²+(y+1)²=4 mit y>= -1,

Kreisgleichung! Radius r = 2 und Mittelpunkt M(2|-1) .

Ergänzung Skizze: https://www.wolframalpha.com/input/?i=(x-2)%5E2%2B(y%2B1)%5E2%3D4+,+y%3E%3D+-1

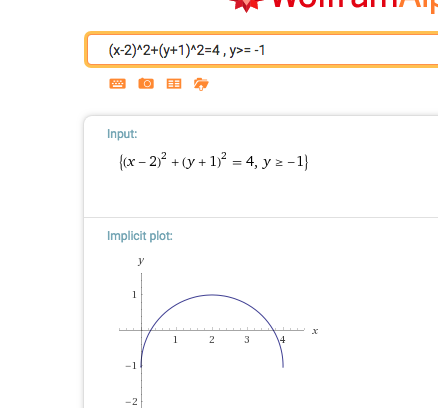
Es gilt auch y≤ 1. Damit nicht surjektiv. Auch nicht injektiv, da gewisse Funktionswerte zweifach angenommen werden.

4. y=x²+2x+2

Parabelgleichung.

Parabel nach oben geöffnet. Es kommen nicht alle neg. Zahlen als Funktionswerte vor ==> nicht surj.

Nicht inj., da Funktionswerte oberhalb des Scheitelpunktes zweimal angenommen werden.

5. y=x³

Endlich gelten die Eigenschaften. bijektiv. surj, und inj.

Comments

Die Ausführungen zum dritten Punkt sind nicht richtig.

---

Danke. Ich hätte zeichnen sollen. Nun besser ?

---

Ja, sehr hübsch! :-)