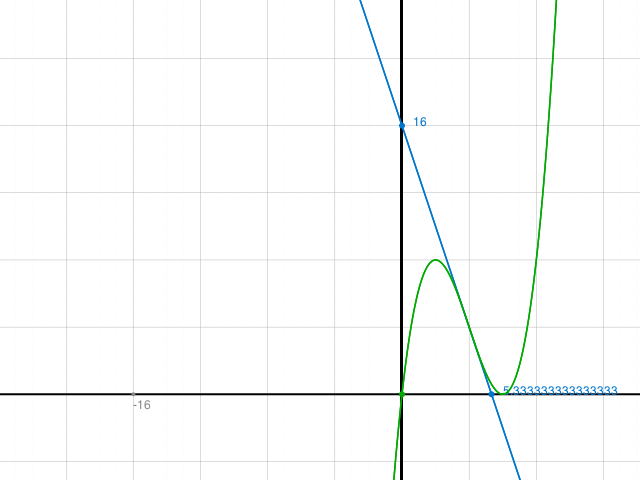
Berechnen Sie den Inhalt der Fläche, die vom Funktionsgraphen, der Wendetangente und der y-Achse begrenzt wird.
Da berechnest du das bestimmte Integral der Differenz der beiden Funktionen von 0 bis x
∫o4 f(x) - t(x) dx. Sollte etwas Negatives rauskommen, nimmst du einfach den Betrag.
Mach aber mal mit dem Funktionsplotter eine Skizze, damit du weisst, was du machst.
Du berechnest das abgerundete Dreieck mit der Ecke E(0|16). Und wirst tatsächlich die negative Fläche rausbekommen, wenn du über f(x) - g(x) integrierst.