f(x) = 1/2·x^3 - 1/8·x^4
f'(x) = 3/2·x^2 - 1/2·x^3
f''(x) = 3·x - 3/2·x^2
Extrempunkt f'(x) = 0
3/2·x^2 - 1/2·x^3 = 0
x = 3 ∨ x = 0
f(3) = 27/8 = 3.375 --> Hochpunkt (3 | 3.375)
Bei 0 haben wir einen Wendepunkt und daher einen Sattelpunkt.
Wendepunkte f''(x) = 0
3·x - 3/2·x^2 = 0
x = 2 ∨ x = 0
f(0) = 0 --> Sattelpunkt (0 | 0)
f(2) = 2 --> Wendepunkt (2 | 2)
Wendetangenten
t1(x) = f'(0) * (x - 0) + f(0) = 0
t2(x) = f'(2) * (x - 2) + f(2) = 2·x - 2
Skizze:
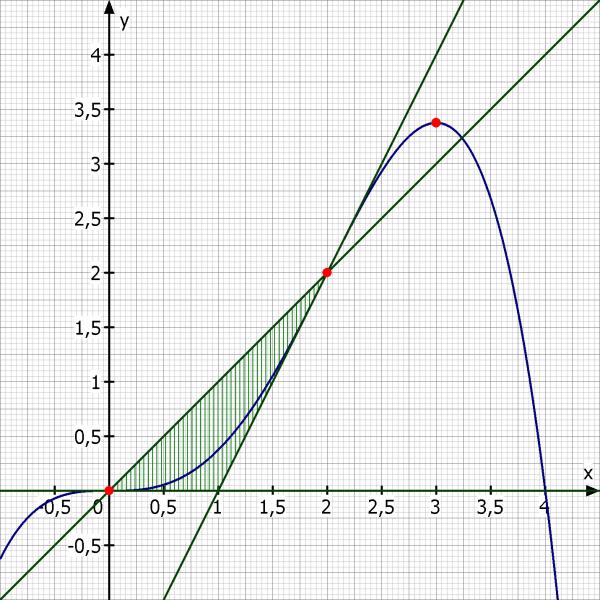
Vom Dreieck sind die Punkte bekannt. Damit kann b) leicht beantwortet werden.
Auch c) kann über die Nullstellen von f(x) leicht beantwortet werden.
Probierst du also den Rest alleine zu beantworten?